Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

z C B O A D y S x M N
a. Do ABCD là hình thoi có tâm là O nên từ giả thiết ta có :
\(C=\left(-2;0;0\right)\)
\(D=\left(0;-1;0\right)\)
Từ đó M là trung điểm của SC nên :
\(M\left(-1;0=-\sqrt{2}\right)\)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{BM}=\left(-1;-1;\sqrt{2}\right)\)
Gọi \(\alpha\) là góc giữa 2 đường thẳng SA, MB, ta có :
\(\cos\alpha=\frac{\left|\overrightarrow{SA.}\overrightarrow{BM}\right|}{\left|\overrightarrow{SA}\right|.\left|\overrightarrow{MB}\right|}=\frac{\left|-2-4\right|}{\sqrt{4+8}.\sqrt{1+2+1}}=\frac{6}{4\sqrt{3}}=\frac{\sqrt{3}}{2}\)
Vậy \(\alpha=60^0\)
Để tính khoảng cách giữa 2 đường thẳng chéo nhau SA, BM ta sử dụng công thức :
\(d\left(SA;BM\right)=\frac{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}\right|}{\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|}\) (1)
Theo công thức xác định tọa độ vecto \(\left[\overrightarrow{SA};\overrightarrow{BM}\right]\) ta có :
\(\left[\overrightarrow{SA};\overrightarrow{BM}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}2&0\\-1&-1\end{matrix}\right|\right)\)
\(=\left(-2\sqrt{2};1;0\right)\)
\(\Rightarrow\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right]\right|=\sqrt{12}\)
\(\overrightarrow{AB}=\left(-2;1;0\right)\)
\(\Rightarrow\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{AB}=4\sqrt{2}\)
Thay vào (1) ta có :
\(d\left(SA;BM\right)=\frac{4\sqrt{2}}{\sqrt{12}}=\frac{2\sqrt{6}}{3}\)
b. Vì AB \\ mặt phẳng (SDC) nên MN \\ DC. Suy ra N là trung điểm của SD
\(\Rightarrow N=\left(0;-\frac{1}{2};\sqrt{2}\right)\)
Dễ thấy :
\(V_{S.ABMN}=V_{S.ABN}+V_{S.BMN}\)
\(=\frac{1}{6}\left|\left[\overrightarrow{SA};\overrightarrow{BM}\right].\overrightarrow{SN}\right|+\frac{1}{6}\left|\left[\overrightarrow{SB};\overrightarrow{SM}\right].\overrightarrow{SN}\right|\) (2)
Ta có \(\overrightarrow{SA}=\left(2;0;-2\sqrt{2}\right)\)
\(\overrightarrow{SN}=\left(0;-\frac{1}{2};-\sqrt{2}\right)\)
\(\overrightarrow{SB}=\left(0;1;-2\sqrt{2}\right)\)
\(\overrightarrow{SM}=\left(-1;0;-\sqrt{2}\right)\)
Ta lại có :
\(\left[\overrightarrow{SA};\overrightarrow{SB}\right]=\left(\left|\begin{matrix}0&-2\sqrt{2}\\-1&-2\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&2\\-2\sqrt{2}&0\end{matrix}\right|;\left|\begin{matrix}2&0\\0&1\end{matrix}\right|\right)\)
\(=\left(2\sqrt{2};4\sqrt{2};2\right)\)
\(\left[\overrightarrow{SB};\overrightarrow{SM}\right]=\left(\left|\begin{matrix}1&-2\sqrt{2}\\0&\sqrt{2}\end{matrix}\right|;\left|\begin{matrix}-2\sqrt{2}&0\\-\sqrt{2}&-1\end{matrix}\right|;\left|\begin{matrix}0&1\\-1&0\end{matrix}\right|\right)\)
\(=\left(-\sqrt{2};2\sqrt{2};1\right)\)
Thay vào (2) được :
\(V_{S.ABMN}=\frac{1}{6}\left(\left|-2\sqrt{2}-2\sqrt{2}\right|+\left|-\sqrt{2}-\sqrt{2}\right|\right)=\sqrt{2}\)

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:
* Tương tự, trục Oy có phương trình
Trục Oz có phương trình
b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:
tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:
phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là
c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là
có phương trình chính tắc là
d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là
và có phương tình chính tắc là

Xem hình cho dễ trả lời nè https://kenh14cdn.com/thumb_w/620/2018/8/31/photo-1-15356853370631011068279.jpg

Gọi B(x;y), ta có \(OA\perp OC\) nên OABC là hình chữ nhật =>\(\overrightarrow{AB}=\overrightarrow{OC}\) \(\Leftrightarrow\begin{cases}x-2=0\\y-0=4\\z-0=0\end{cases}\) \(\Rightarrow B\left(2;4;0\right)\)
Ta có \(\overrightarrow{OB}=\left(2;4;0\right);\overrightarrow{OD}=\left(0;0;4\right);\overrightarrow{CB}=\left(2;0;0\right);\overrightarrow{CD}=\left(0;-4;4\right)\)
Do đó \(\overrightarrow{OB}.\overrightarrow{OD}=0\) và \(\overrightarrow{CB}.\overrightarrow{CD}=0\Rightarrow\widehat{BOD}=\widehat{BCD}=90^0\)
Suy ra mặt cầu đi qua 4 điểm O, B, C, D có tâm I là trung điểm của BD, bán kính R=OI
Ta có \(I\left(1;2;2\right);R=OI=\sqrt{1+2^2+2^2}=3\)
Do đó mặt cầu (S) có phương trình : \(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-2\right)^2=9\)
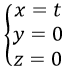
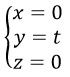
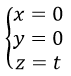
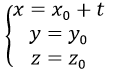
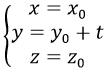
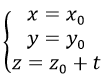
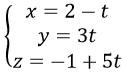
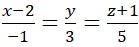
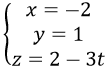
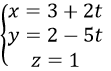
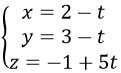
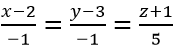

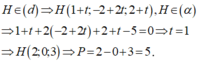
Đáp án D