Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=2\left(1+2\right)+2^3\left(1+2\right)+2^5\left(1+2\right)+2^7\left(1+2\right)+2^9\left(1+2\right)\)
\(=3\left(2+2^3+2^5+2^7+2^9\right)⋮3\)

Ta có :
\(2+2^2+2^3+....+2^{10}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+....+2^9\left(1+2\right)\)
\(=2.3+2^3.3+....+2^9.3\)
=> Tổng chia hết cho 3
\(2+2^2+2^3+...+2^{10}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^9+2^{10}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^9\left(1+2\right)\)
\(=2.3+2^3.3+...+2^9.3\)
\(=\left(2+2^3+...+2^9\right).3⋮3\)
\(\Rightarrow2+2^2+2^3+...+2^{10}⋮3\)

\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^9+2^{10}\right)\)
\(A=2.\left(1+2\right)+2^3.\left(1+2\right)+...+2^9.\left(1+2\right)\)
\(A=2.3+2^3.3+...+2^9.3\)
\(A=3.\left(2+2^3+...+2^9\right)⋮3\)
A = 2 + 22 +...+ 210 ( có 10 số hạng)
A = (2+22 ) +( 23+24) + ...+ (29+210)
A = 2.(1+2) + 23.(1+2) + ...+ 29.(1+2)
A = 2.3 + 23.3 + ...+ 29.3
A = 3.(2+23 +...+29) chia hết cho 3

Ta có 2A=22+23+...+211
=>2A-A=(22+23+...+211)-(2+22+23+...+210)
=>A=211-2=2.(210-1)
=2.1024-1=2.1023
Do 1023 chia hết cho 3=>A chia hết cho 3
A có 10 số hạng, ta chia A thành 5 nhóm, mỗi nhóm có 2 số hạng như sau:
A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
= (2 + 22) + (23 + 24) + (25 + 26) + (27 + 28) + (29 + 210)
= 2(1 + 2) + 23(1 + 2) + 25(1 + 2) + 27(1 + 2) + 29(1 + 2)
= 2.3 + 23.3 + 25.3 + 27.3 + 29.3
= (2 + 23 + 25 + 27 + 29).3 \(⋮\) 3
Vậy A \(⋮\) 3

b1:
B=3+3^2+...+3^60=(3+3^2+3^3)+...+(3^58+3^59+3^60)=3(1+3+3^2)+...+3^58(1+3+3^2)=3*13+...+3^58*13=13(3+...+3^58) (CHIA HẾT CHO 13)
A=5+5^2+...+5^10=(5+5^2)+(5^3+5^4)+...+(5^9+5^10)=5(1+5)+...+5^9(1+5)=5*6+...+5^9*6=(5+...+5^9)*6(CHIA HẾT CHO 6)
B2: bạn kéo xuống dưới nãy mk thấy có ng làm r
b3: (2x+1)(y-5)=168
Ta có bảng sau:
| 2x+1 | 1 | 2 | 4 | 7 | 8 | 12 | 14 | 21 | 24 | 42 | 84 | 168 |
| 2x | 0 | 1 | 3 | 6 | 7 | 11 | 13 | 20 | 23 | 41 | 83 | 167 |
| x | 0 | 3 | 10 | |||||||||
| y-5 | 168 | 24 | 8 | |||||||||
| y | 173 | 29 | 13 |
(mấy ô mk để trống là loại vì x,y là số tự nhiên)
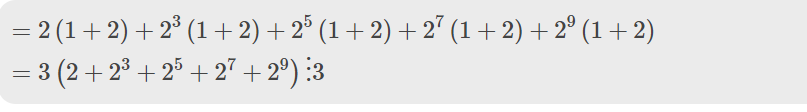
Ta có: A=(3+3^2)+(3^3+3^4)+..+(3^9+3^10)
=3.(1+3)+3^3.(1+3)+..+3^9.(1+3)
=3.4+3^3.4+..+3^9.4
=4.(3+3^3+..+3^9) ( hết cho 4)
Vậy A chia hết cho 4