
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=2\cdot\left(sinx\right)'\cdot sinx+3\cdot\left(-2x\right)\cdot sin2x\)
\(=2cosx\cdot sinx-6x\cdot sin2x=sin2x\cdot\left(1-6x\right)\)

1/ \(y'=\left(1-3x\right)'\sqrt{x-3}+\left(1-3x\right)\left(\sqrt{x-3}\right)'=-3\sqrt{x-3}+\dfrac{1}{2\sqrt{x-3}}\left(1-3x\right)\)
2/ \(y'=\dfrac{1}{\sqrt{2x+1}}-\dfrac{1}{\left(x+1\right)^2}\)
3/ \(y'=\dfrac{1}{2}.\sqrt{\dfrac{1+x}{1-x}}.\left(\dfrac{1-x}{1+x}\right)'=\dfrac{1}{2}\sqrt{\dfrac{1+x}{1-x}}.\dfrac{-2}{\left(1+x\right)^2}=-\sqrt{\dfrac{1+x}{1-x}}.\dfrac{1}{\left(1+x\right)^2}\)
4/ \(y'=\left(\cos5x\right)'.\cos7x+\cos5x.\left(\cos7x\right)'=-5\sin5x.\cos7x-7\cos5x\sin7x\)
5/ \(y'=\left(\cos x\right)'\sin^2x+\cos x\left(\sin^2x\right)'=-\sin^3x+2\sin x.\cos^2x\)
6/ \(y'=\left(\tan^42x\right)'=4.\tan^32x.\dfrac{2}{\cos^22x}\)
7/ \(y'=\dfrac{2\sin x+2\cos x-2x.\cos x+2x\sin x}{\left(\sin x+\cos x\right)^2}\)
Ờm, bạn tự rút gọn nhé :) Mình đang hơi lười :b
Tìm đạo hàm của hàm số \(y=\dfrac{a^3}{\sqrt{a^2-x^2}}\) (a là hằng số)
Giúp mình với ạ, mình cảm ơnn

\(y'=\dfrac{\left(a^3\right)'.\sqrt{a^2-x^2}-\left(\sqrt{a^2-x^2}\right)'.a^3}{a^2-x^2}=\dfrac{-\dfrac{1}{2\sqrt{a^2-x^2}}\left(a^2-x^2\right)'.a^3}{a^2-x^2}\)
\(y'=\dfrac{x.a^3}{\sqrt{a^2-x^2}\left(a^2-x^2\right)}\)

\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)

\(\sqrt[n]{y}=4x+1\)
\(y^{\dfrac{1}{n}}=4x+1\)
đạo cấp 1
\(\dfrac{1}{n}y^{\left(\dfrac{1}{n}-1\right)}=\dfrac{1}{n}\sqrt[n]{y^{\left(1-n\right)}}=4\)
thay y=(4x+1)^n vào
\(\dfrac{1}{n}\sqrt[n]{\left(4x+1\right)^{n\left(1-n\right)}}=\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}\)
từ đó: \(y'=\dfrac{4}{\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}}=4.n\left(4x+1\right)^{n-1}\)
Có đúng không: cấp n có thể phải làm lấy vài cái--> quy luật nào đó

a.\(y'=x\left(\sqrt{x^2-2x}\right)'+\sqrt{x^2-2x}=\dfrac{x}{2\sqrt{x^2-2x}}2\left(x-1\right)+\sqrt{x^2-2x}=\dfrac{x\left(x-1\right)}{\sqrt{x^2-2x}}+\sqrt{x^2-2x}\)
\(=\dfrac{x^2-x+x^2-2x}{2\sqrt{x^2-2x}}=\dfrac{2x^2-3x}{2\sqrt{x^2-2x}}\)
b. \(y=3sin2x+cos3x\Rightarrow y'=6cos2x-3sin3x\)

a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
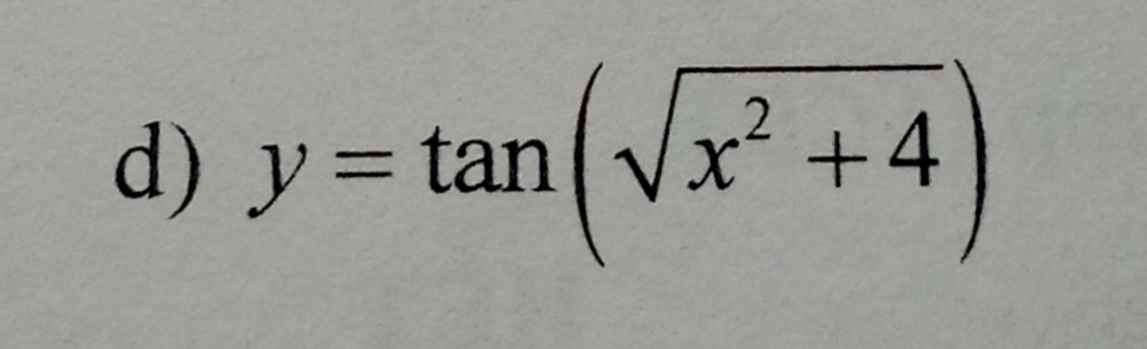
\(y'=\dfrac{1}{2\sqrt{x-1}}+7\cdot x^6\)