DC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 1 2022
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;1\right\}\end{matrix}\right.\)
Ta có: \(A=\dfrac{x-4\sqrt{x}+3-\left(2x-4\sqrt{x}-\sqrt{x}+2\right)+x+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2x-4\sqrt{x}+5-2x+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
17 tháng 12 2023
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{1;4\right\}\end{matrix}\right.\)
\(A=\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{x-3\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)-\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-4\sqrt{x}+3-2x+5\sqrt{x}-2+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}=\dfrac{1}{\sqrt{x}-2}\)
b: Để A>2 thì A-2>0
=>\(\dfrac{1-2\left(\sqrt{x}-2\right)}{\sqrt{x}-2}>0\)
=>\(\dfrac{5-2\sqrt{x}}{\sqrt{x}-2}>0\)
=>\(\dfrac{2\sqrt{x}-5}{\sqrt{x}-2}< 0\)
TH1: \(\left\{{}\begin{matrix}2\sqrt{x}-5>0\\\sqrt{x}-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>\dfrac{5}{2}\\\sqrt{x}< 2\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}2\sqrt{x}-5< 0\\\sqrt{x}-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}< \dfrac{5}{2}\\\sqrt{x}>2\end{matrix}\right.\)
=>\(2< \sqrt{x}< \dfrac{5}{2}\)
=>4<x<25/4
c: Để A là số nguyên thì \(1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{1;9\right\}\)
kết hợp ĐKXĐ, ta được: x=9
24 tháng 8 2016
P = AB = \(\frac{3\sqrt{x}}{\sqrt{x}+1}\)= 3 - \(\frac{3}{\sqrt{x}+1}\)
Để P nguyên thì \(1+\sqrt{x}\)phải là ước của 3 hay \(1+\sqrt{x}\)= (1;3)
Thế vào giải ra
27 tháng 11 2018
\(Q=\frac{\sqrt{x}\cdot\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\frac{\sqrt{x}\cdot\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\frac{2\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
\(Q=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(Q=x+1\)
Không thể tìm được GTLN hay GTNN của Q.
b)
\(\frac{3x+3}{\sqrt{x}}=3\sqrt{x}+\frac{3}{\sqrt{x}}\)
Để \(\frac{3Q}{\sqrt{x}}\) nguyên thì \(\frac{3}{\sqrt{x}}\)nguyên hay \(\sqrt{x}\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Vì \(\sqrt{x}\)dương nên \(\sqrt{x}\in\left\{1;3\right\}\)
Vậy x=1, x=9 là các giá trị cần tìm
7 tháng 9 2020
a, \(P=\frac{\sqrt{x}+2}{\sqrt{x}+1}-\frac{\sqrt{x}+3}{5-\sqrt{x}}-\frac{3x+4\sqrt{x}-5}{x-4\sqrt{x}-5}\)
\(P=\frac{\sqrt{x}+2}{\sqrt{x}+1}+\frac{\sqrt{x}+3}{\sqrt{x}-5}-\frac{3x+4\sqrt{x}-5}{x-4\sqrt{x}-5}\)
\(P=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}+\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}-\frac{3x+4\sqrt{x}-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}\)
\(P=\frac{x-3\sqrt{x}-10+x+4\sqrt{x}+3-3x-4\sqrt{x}+5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}\)
\(P=\frac{-x-3\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}\)
\(P=\frac{\left(\sqrt{x}+1\right)\left(-\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-5\right)}=\frac{-\sqrt{x}-2}{\sqrt{x}-5}\)
để P > -2
\(\Rightarrow\frac{-\sqrt{x}-2}{\sqrt{x}-5}>-2\) đoạn này đang chưa nghĩ ra
c, \(P=\frac{-\sqrt{x}-2}{\sqrt{x}-5}\in Z\) \(\Rightarrow-\sqrt{x}-2⋮\sqrt{x}-5\)
=> -căn x + 5 - 7 ⋮ căn x - 5
=> -(căn x - 5) - 7 ⋮ căn x - 5
=> 7 ⋮ x - 5 đoạn này dễ
8 tháng 9 2020
a, Với \(x\ge0;x\ne25\)thì \(P=\frac{\sqrt{x}+2}{5-\sqrt{x}}\) đoạn này đúng rồi
\(P>-2\)\(\Leftrightarrow\frac{\sqrt{x}+2}{5-\sqrt{x}}>-2\)
\(\Leftrightarrow\frac{\sqrt{x}+2}{5-\sqrt{x}}+2>0\)
\(\Leftrightarrow\frac{12-\sqrt{x}}{5-\sqrt{x}}>0\)
Xét 2 trường hợp cùng âm, cùng dương hoặc "trong trái ngoài cùng"
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}>12\\0\le\sqrt{x}< 5\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}x>144\\0\le x< 25\end{cases}}\)
Làm luôn cho đầy đủ =)
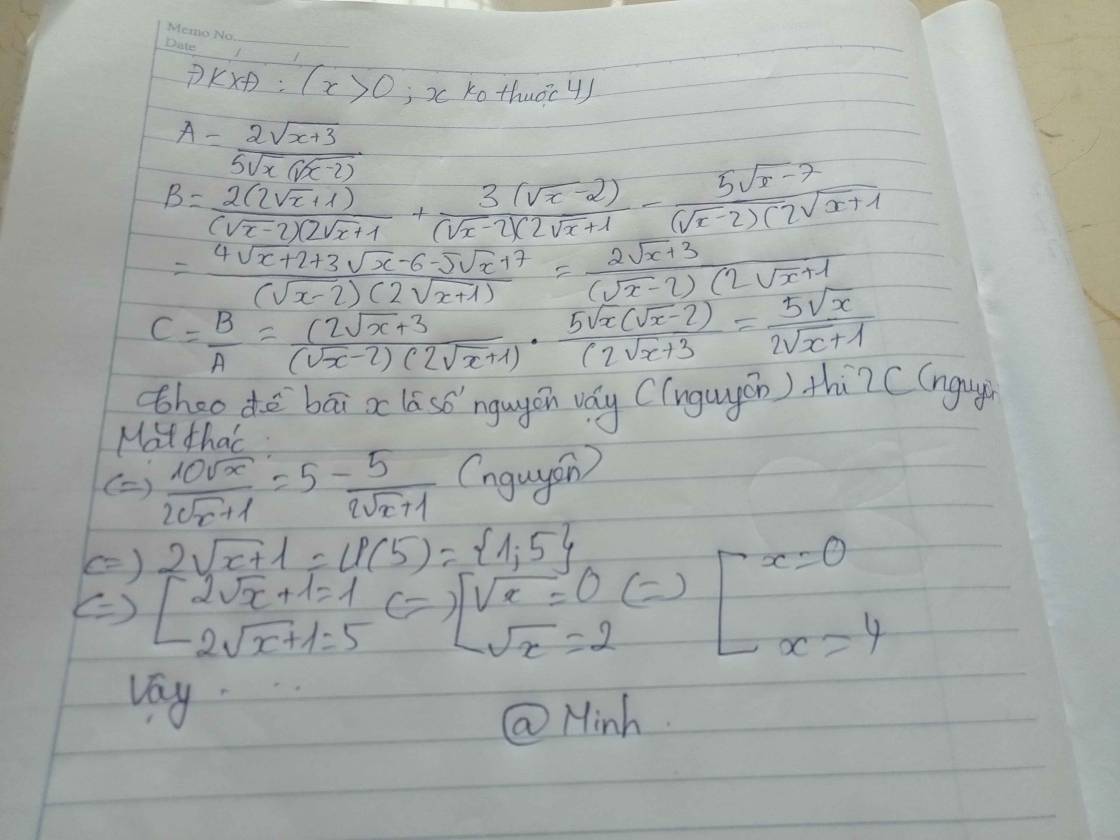
Lời giải:
\(\frac{3\sqrt{x}}{\sqrt{x}-3}=\frac{3(\sqrt{x}-3)+9}{\sqrt{x}-3}=3+\frac{9}{\sqrt{x}-3}\)
Để biểu thức đã cho nguyên thì $\frac{9}{\sqrt{x}-3}$ nguyên. Đặt $\frac{9}{\sqrt{x}-3}=t$ với $t$ nguyên.
$\sqrt{x}=\frac{9}{t}+3$
Do $\sqrt{x}\geq 0$ nên $\frac{9}{t}+3\geq 0\Leftrightarrow \frac{3(3+t)}{t}\geq 0$
$\Leftrightarrow t>0$ hoặc $t\leq -3$
$x=(\frac{9}{t}+3)^2$ với $t$ là số nguyên thỏa mãn $t>0$ hoặc $t\leq -3$
A =\(\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
A = \(\dfrac{3\sqrt{x}-3+3}{\sqrt{x}-3}\)= 3 -\(\dfrac{3}{\sqrt{x}-3}\)
Để A nguyên thì : 3 \(⋮\)\(\sqrt{x}\) - 3
\(\sqrt{x}\) - 3 \(\in\) \(\left\{-3;-1;1;3\right\}\)
\(\sqrt{x}\) - 3 = -3 \(\Rightarrow\) \(x\) = 0
\(\sqrt{x}\) - 3 = -1 \(\Rightarrow\) \(x\) = 4
\(\sqrt{x}\) - 3 = 1 \(\Rightarrow\) \(x\) = 16
\(\sqrt{x}\) - 3 = 3 \(\Rightarrow\) \(x\)= 36
kết luận \(x\)\(\in\) \(\left\{0;4;16;36\right\}\)