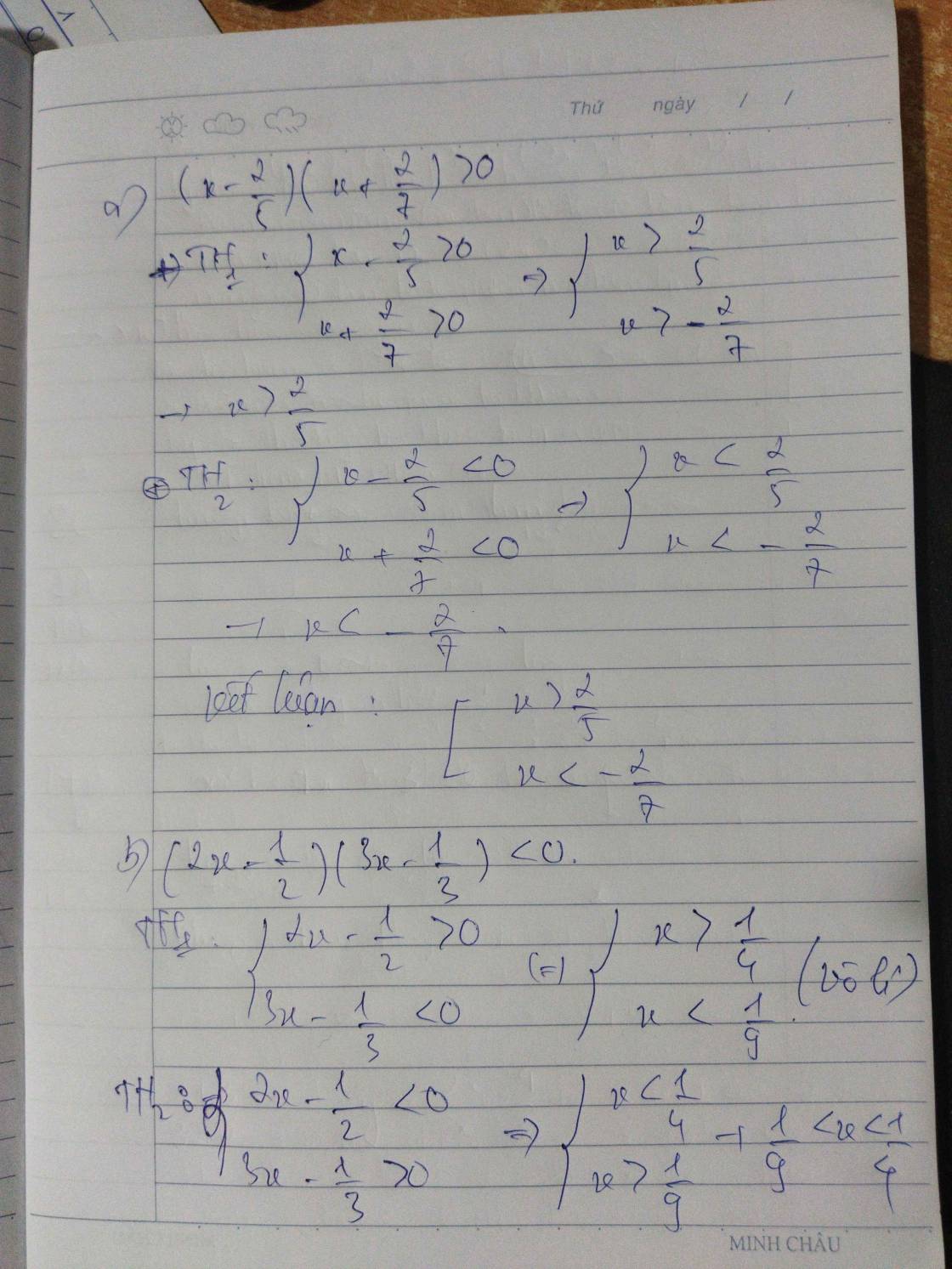tìm x : a, x-2/5).(x+2/7)>0 b,(2x-1/2).(3x-1/3)<0

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TT

Trần tường Vy

2 tháng 10 2023 - olm

tìm x : a, x-2/5).(x+2/7)>0 b,(2x-1/2).(3x-1/3)<0

#Hỏi cộng đồng OLM #Toán lớp 7

1

DT

Dang Tung

CTVHS

2 tháng 10 2023

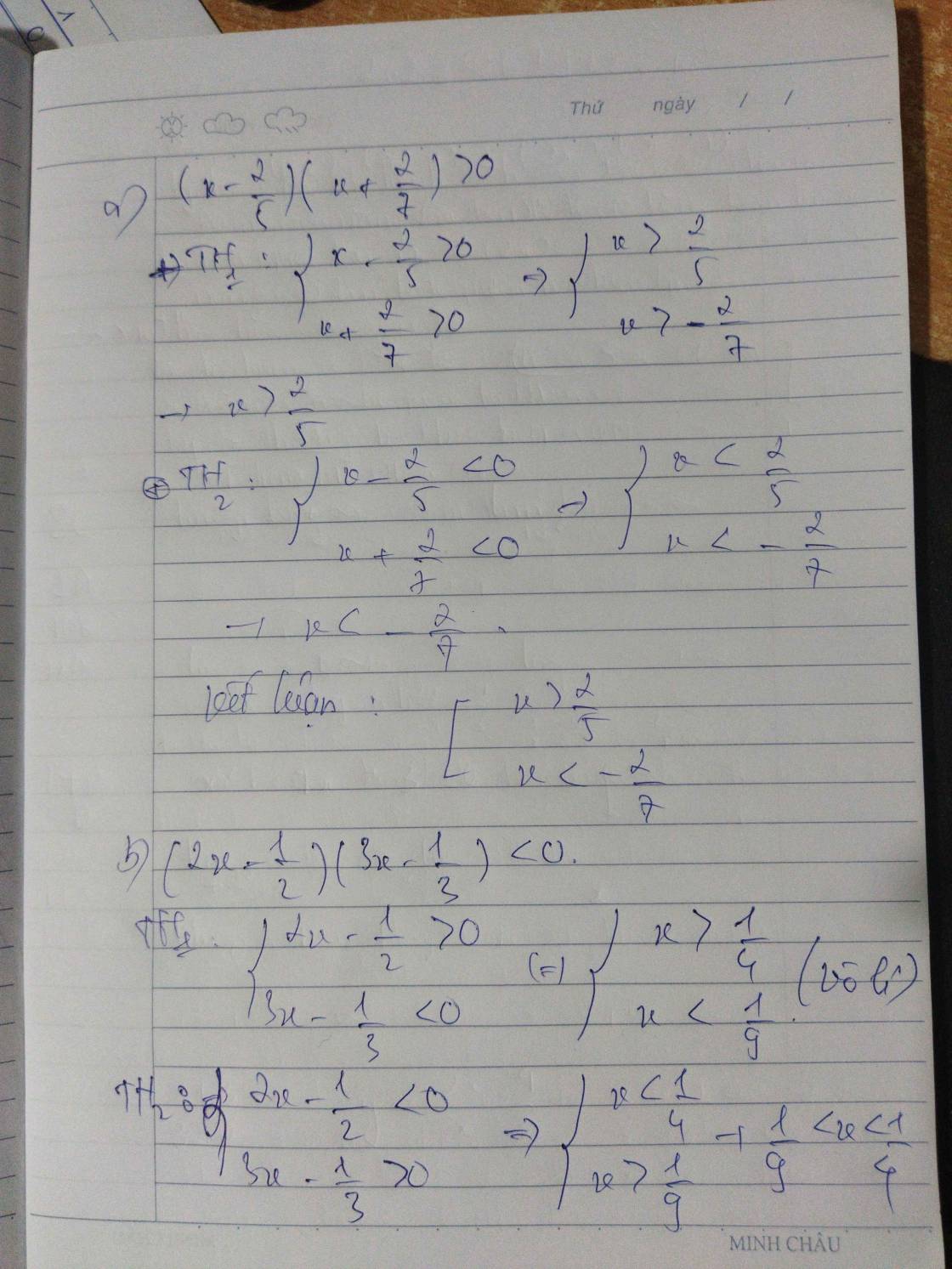loading... Bạn tham khảo.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PV

Phan Viết Học

26 tháng 9 2017 - olm

Tìm x biết

a. (x - 2).(x + 3/4) > 0

b. (2x - 5).(1 - 3x) > 0

c. (3 - 2x).(x + 1) < 0

d.(5x + 11).(7 - x) < 0

#Hỏi cộng đồng OLM #Toán lớp 7

10

DN

đỗ ngọc ánh

26 tháng 9 2017

toán lớp 7 mà đã học bpt hướng dẫn * tích lớn hơn 0 nên 2 nhân tử cùng dấu ( cùng + or cùng -) * <) thì trái dấu 1+;1-

DN

đỗ ngọc ánh

26 tháng 9 2017

nếu >0 thì hai nhân tử cùng dấu

<0 thì trái dấu

DQ

Đỗ Quỳnh Anh

24 tháng 8 2015 - olm

Tìm x: a) (x^2+3).(x-5)<0. ; b) (-x^2-1).(2x-1)>0. ; c) (|x|+3).(1/2+3x)>0 ; d) (2|x|-1).(7-3x)=0

#Hỏi cộng đồng OLM #Toán lớp 7

0

TU

Ta Uyen Chi

19 tháng 9 2015 - olm

Bt1 tìm x

a) (3/x+1/5).(x-1/2)=0

b)(x-3/2).(2x+1)>0

c)(x-2).(x-4)<0

d)(3x+1/5).(2x-1)<0

e)(x-1).(3x-5)<0

#Hỏi cộng đồng OLM #Toán lớp 7

0

VT

Vũ Thùy Trang

22 tháng 7 2015 - olm

Tìm x biết :
a. 3(2x+3)(3x-5)<0 ; b. x²+1>0 ; c. (x²+1)(2x-5)>0 ; d. x²+2x<0

#Hỏi cộng đồng OLM #Toán lớp 7

0

CY

Chibi Yoona

1 tháng 8 2017

a.(2x-3) (3x+6) > 0

b.(3x+4) (2x-6) < 0

c.(3x+5) (2x+4) > 4

d.(3x+4) (x-2) <0

e.(x+4) (2x-4) > 0

f.(4x-8) (2x+5) < 0

g.(2x-3) (3x+6) _> 0

h.(3x-7) (x+1) <_ 0

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 5 2022

a: (2x-3)(3x+6)>0

=>(2x-3)(x+2)>0

=>x<-2 hoặc x>3/2

b: (3x+4)(2x-6)<0

=>(3x+4)(x-3)<0

=>-4/3<x<3

c: (3x+5)(2x+4)>4

\(\Leftrightarrow6x^2+12x+10x+20-4>0\)

\(\Leftrightarrow6x^2+22x+16>0\)

=>\(6x^2+6x+16x+16>0\)

=>(x+1)(3x+8)>0

=>x>-1 hoặc x<-8/3

f: (4x-8)(2x+5)<0

=>(x-2)(2x+5)<0

=>-5/2<x<2

h: (3x-7)(x+1)<=0

=>x+1>=0 và 3x-7<=0

=>-1<=x<=7/3

TT

Thiên Thu Nguyệt

20 tháng 8 2015 - olm

Tìm x:

a) (x^2+3).(x-5)<0. ;

b) ( -x^2-1).(2x-1)>0. ;

c) (|x|+3).(1/2+3x)>0

#Hỏi cộng đồng OLM #Toán lớp 7

1

S

sakura

20 tháng 8 2015

nếu tích 2 số < 0 thì có 2 trường hợp xảy ra là số thứ nhất âm số thứ 2 duong và ngược lại

nếu tích 2 số > 0 thì có 2 trường hợp là cả 2 số cùng dương hoặc cùng âm

S

Steven

12 tháng 9 2020 - olm

Tìm x:

a) (x - 2/5).(x+2/7)>0

b) (2x-1/2).(3x-1/3)<0

#Hỏi cộng đồng OLM #Toán lớp 7

2

TT

Trí Tiên

12 tháng 9 2020

\(\left(x-\frac{2}{5}\right)\left(x+\frac{2}{7}\right)>0\)

\(\Leftrightarrow\orbr{\begin{cases}x-\frac{2}{5}>0\\x+\frac{2}{7}>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x>\frac{2}{5}\\x>-\frac{2}{7}\end{cases}\Leftrightarrow}x>\frac{2}{5}}\)

\(\Leftrightarrow\orbr{\begin{cases}x-\frac{2}{5}< 0\\x+\frac{2}{7}< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< \frac{2}{5}\\x< -\frac{2}{7}\end{cases}\Leftrightarrow}x< -\frac{2}{7}}\)

b) \(\left(2x-\frac{1}{2}\right)\left(3x-\frac{1}{3}\right)< 0\)

\(\Leftrightarrow\orbr{\begin{cases}2x-\frac{1}{2}>0\\3x-\frac{1}{3}< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>\frac{1}{4}\\x< \frac{1}{9}\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}2x-\frac{1}{2}< 0\\3x-\frac{1}{3}>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< \frac{1}{4}\\x>\frac{1}{9}\end{cases}}\)

LD

l҉o҉n҉g҉ d҉z҉

12 tháng 9 2020

a) ( x - 2/5 )( x + 2/7 ) > 0

Xét hai trường hợp :

1. \(\hept{\begin{cases}x-\frac{2}{5}>0\\x+\frac{2}{7}>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>\frac{2}{5}\\x>-\frac{2}{7}\end{cases}\Leftrightarrow}x>\frac{2}{5}\)

2. \(\hept{\begin{cases}x-\frac{2}{5}< 0\\x+\frac{2}{7}< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< \frac{2}{5}\\x< -\frac{2}{7}\end{cases}}\Leftrightarrow x< -\frac{2}{7}\)

Vậy với x > 2/5 hoặc x < -2/7 thì ( x - 2/5 )( x + 2/7 ) > 0

b) ( 2x - 1/2 )( 3x - 1/3 ) < 0

Xét hai trường hợp :

1. \(\hept{\begin{cases}2x-\frac{1}{2}>0\\3x-\frac{1}{3}< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x>\frac{1}{2}\\3x< \frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}x>\frac{1}{4}\\x< \frac{1}{9}\end{cases}}\)( loại )

2. \(\hept{\begin{cases}2x-\frac{1}{2}< 0\\3x-\frac{1}{3}>0\end{cases}\Leftrightarrow}\hept{\begin{cases}2x< \frac{1}{2}\\3x>\frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}x< \frac{1}{4}\\x>\frac{1}{9}\end{cases}}\Leftrightarrow\frac{1}{9}< x< \frac{1}{4}\)

Vậy với 1/9 < x < 1/4 thì ( 2x - 1/2 )( 3x - 1/3 ) < 0

P

Pikachu

25 tháng 2 2017

Bài 2 : Tìm x thuộc Z

a) ( 3x + 1 ) ( 2x - 4 ) < 0

b) ( -x - 5 ) ( 2x + 1 ) > 0
c) ( x - 7 ) ( x + 1 ) < 0
d) | x + 3 | < 5

e) | 2x - 3 | < 1

#Hỏi cộng đồng OLM #Toán lớp 7

3

HT

Hoàng Thị Ngọc Anh

25 tháng 2 2017

Làm câu a và b thoy nhé, câu c tương tự câu a, câu d và e thì dễ rồi.

a) Vì \(\left(3x+1\right)\left(2x-4\right)< 0\)

\(\Rightarrow3x+1>0\) và \(2x-4< 0\)

hoặc \(3x+1< 0\) và \(2x-4>0\)

+) \(3x+1>0\Rightarrow x>\frac{-1}{3}\left(1\right)\)

\(2x-4< 0\Rightarrow x< 2\left(2\right)\)

Từ (1) và (2) suy ra \(\frac{-1}{3}< x< 2\)

+) \(3x+1< 0\Rightarrow x< \frac{-1}{3}\left(3\right)\)

\(2x-4>0\Rightarrow x>2\left(4\right)\)

Từ (3) và (4) suy ra \(2< x< \frac{-1}{3}\)

\(\Rightarrow\) vô lý.

Vậy \(\frac{-1}{3}< x< 2.\)

b) Do \(\left(-x-5\right)\left(2x+1\right)>0\)

\(\Rightarrow-x-5>0\) và \(2x+1>0\)

hoặc \(-x-5< 0\) và \(2x+1< 0\)

+) \(-x-5>0\Rightarrow x>-5\left(5\right)\)

\(2x+1>0\Rightarrow x>\frac{-1}{2}\left(6\right)\)

Từ (5) và (6) suy ra \(x>\frac{-1}{2}\)

+) \(-x-5< 0\Rightarrow x< -5\left(7\right)\)

\(2x+1< 0\Rightarrow x< \frac{-1}{2}\) (8)

Từ (7) và (8) suy ra \(x< -5\)

Vậy \(\left[\begin{matrix}x>\frac{-1}{2}\\x< -5\end{matrix}\right.\).

NT

Nguyễn Thị Thảo

25 tháng 2 2017

d)\(\left|x+3\right|< 5\)

\(\Rightarrow-5< x+3< 5\)

\(\Rightarrow-8< x< 2\)

KP

Khải Phan

26 tháng 9 2017

Tìm x biết:

a. (x - 2).(x + 3/4) > 0

b. (2x - 5).(1 - 3x) > 0

c. (3 - 2x).(x + 1) < 0

d.(5x + 11).(7 - x) < 0

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 5 2022

a: (x-2)(x+3/4)>0

=>x-2>0 hoặc x+3/4<0

=>x>2 hoặc x<-3/4

b: (2x-5)(1-3x)>0

=>(2x-5)(3x-1)<0

=>3x-1>0 và 2x-5<0

=>1/3<x<5/2

c: (3-2x)(x+1)<0

=>(2x-3)(x+1)>0

=>2x-3>0 hoặc x+1<0

=>x>3/2 hoặc x<-1

d: (5x+11)(7-x)<0

=>(5x+11)(x-7)>0

=>x>7 hoặc x<-11/5

NX

Nguyễn Xuân Minh Hằng

21 tháng 9 2021 - olm

Các bạn giải rõ ràng ra giúp mình nhé, làm bao nhiêu câu cx đc, hết càng tốt. Ngày mai mình nộp bài gòi. Thx các bạn trc <3
Bài: Tìm x, biết:
1/ (x - 6).(2x + 10) > 0
2/ (2x - 8).(x - 2) < 0
3/ (3x - 1) / (x + 2) < hoặc = 0
4/ (4x + 3) / (2x - 5) > 0
5/ (x + 5) / (x + 3) < 1
6/ (x - 7)^x+1 = (x - 7)^x+11

#Hỏi cộng đồng OLM #Toán lớp 7

0