K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
29 tháng 1 2020
a) Ta có : 3n+40\(⋮\)n+4
\(\Rightarrow\)3n+12+28\(⋮\)n+4
\(\Rightarrow\)3(n+4)+28\(⋮\)n+4
Vì 3(n+4)\(⋮\)n+4 nên 28\(⋮\)n+4
\(\Rightarrow n+4\inƯ\left(28\right)=\left\{\pm1;\pm2\pm4;\pm7;\pm14;\pm28\right\}\)
+) n+4=-1\(\Rightarrow\)-5 (không thỏa mãn)
+) n+4=1\(\Rightarrow\)n=-3 (không thỏa mãn)
+) n+4=-2\(\Rightarrow\)n=-6 (không thỏa mãn)
+) n+4=2\(\Rightarrow\)n=-2 (không thỏa mãn)
+) n+4=-4\(\Rightarrow\)n=-8 (không thỏa mãn)
+) n+4=4\(\Rightarrow\)n=0 (thỏa mãn)
+) n+4=-7\(\Rightarrow\)n=-11 (không thỏa mãn)
+) n+4=7\(\Rightarrow\)n=3 (thỏa mãn)
+) n+4=-14\(\Rightarrow\)n=-18 (không thỏa mãn)
+) n+4=14\(\Rightarrow\)n=10 (thỏa mãn)
+) n+4=-28\(\Rightarrow\)n=-32 (không thỏa mãn)
+) n+4=28\(\Rightarrow\)n=24 (thỏa mãn)
Vậy n\(\in\){0;3;10;24}
29 tháng 1 2020
b) Ta có : 5n+2\(⋮\)2n+9
\(\Rightarrow\)10n+4\(⋮\)10n+45
\(\Rightarrow\)10+45-41\(⋮\)10n+45
Vì 10n+45\(⋮\)10n+45 nên 41\(⋮\)10n+45
\(\Rightarrow10n+45\inƯ\left(41\right)=\left\{\pm1;\pm41\right\}\)
+) 10n+45=-1\(\Rightarrow\)10n=-46\(\Rightarrow\)n=\(-\frac{23}{5}\)(không thỏa mãn)
+) 10n+45=1\(\Rightarrow\)10n=-44\(\Rightarrow\)n=\(-\frac{22}{5}\)(không thỏa mãn)
+) 10n+45=-41\(\Rightarrow\)10n=-86\(\Rightarrow\)n=\(-\frac{43}{5}\)(không thỏa mãn)
+) 10n+45=41\(\Rightarrow\)10n=-4\(\Rightarrow\)n=\(-\frac{2}{5}\)(không thỏa mãn)
Vậy không tìm được giá trị của n thỏa mãn bài toán.
NP
1
30 tháng 11 2016
a, Ta có 3(n + 4 ) \(⋮\) (n+ 4)
\(\Rightarrow\) 3(n + 4) = 3n + 12.
Xét tổng (16 - 3n) + (3n + 12)
= 16 - 3n + 3n + 12
= 28 (khử n)
Để (16 - 3n) \(⋮\)(n+4) thì 28 \(⋮\)(n+4)
\(\Rightarrow\) n+ 4\(\in\) Ư(28) = { 1 ; 2 ; 4 ; 7 ; 14 ; 28}
Vì n+ 4 \(\ge\) 4 \(\Rightarrow\) n+4 \(\in\) { 4 ; 7 ; 14 ; 28}
+ n + 4 = 4
n = 4 - 4
n = 0
+ n + 4 = 7
n = 7 - 4
n = 3
+ n + 4 = 14
n = 14 - 4
n = 10
+ n + 4 = 28
n = 28 - 4
n = 24
Vậy n \(\in\) { 0 ; 3 ; 10 ; 24}
b, Làm dạng giống phần a. Hãy động não một chút.
PT
1
CM
30 tháng 7 2017
a, Vì (n+3) ⋮ (n+3) nên để (n+8) ⋮ (n+3) thì: [(n+8) - (n+3)] ⋮ (n+3) hay 5 ⋮ (n+3), Suy ra: n+3 ∈ {1;5}
Vì n + 3 ≥ 3 nên n + 3 = 5 => n = 2
Vậy n = 2
b, Vì 3(n+4) ⋮ (n+4) nên để (16 - 3n) ⋮ (n+4) thì: [(16 - 3n)+3(n+4)] ⋮ (n+4) hay 28 ⋮ (n+4)
Suy ra: n+4 ∈ {1;2;4;7;14;28}
Vì 0 ≤ n ≤6 nên 4 ≤ n+4 ≤ 10.
Từ đó ta có: n+4 ∈ {4;7} hay n ∈ {0;3}
c, Vì 5(9 - 2n) ⋮ (9 - 2n) nên nếu (5n+2) ⋮ (9 - 2n) thì 2(5n+2) ⋮ (9 - 2n)
Suy ra: [5(9 - 2n)+2(5n+2)] ⋮ (9 - 2n) hay 49 ⋮ (9 - 2n) => 9 - 2n ∈ {1;7;49}
Vì 9 - 2n ≤ 9 nên 9 - 2n ∈ {1;7}
Từ đó ta có n ∈ {4;1} với n < 5
Thử lại ta thấy n = 4 hoặc n = 1 đều thõa mãn.
Vậy n ∈ {4;1}
DA
19 tháng 2 2020
B = \(\frac{2n+9}{n+2}\)+ \(\frac{5n+17}{n+2}\)-\(\frac{3n}{n+2}\)
B= \(\frac{2n+9+5n+17-3n}{n+2}\)
B= \(\frac{\left(2n+5n-3n\right)+9+17}{n+2}\)
B= \(\frac{4n+9+17}{n+2}\)= \(\frac{4n+26}{n+2}\)
Để biểu thức B là số tự nhiên thì ( 4n+26) \(⋮\)n+2
=> n+2 \(⋮\)n+2
=> (4n+26) - 4(n+2)\(⋮\)n+2
=> 4n+26 - 4n - 8 \(⋮\)n+2
=> 18 \(⋮\)n+2
=> n+2 \(\in\)Ư(18)={1; 2; 9; 3; 6; 18; -1; -2; -9; -3; -6; -18}
=> N\(\in\){ -1; 0; 7; 1; 4; 16; -3; -4; -5; -11; -20; -8}
Vậy...
11 tháng 10 2017
a) 16 - 3n chia hết cho n +4
n+ 4 chia hết cho n+4
=) (16 - 3n ) - ( n + 4) chia hết cho n + 4
16 - 3n - n- 4 chia hết n + 4
12 +4n chia hết cho n +4
= ) n +4 thuộc Ư ( 12 + 4n )
?????
hic mới biết làm tới đây thông cảm
24 tháng 10 2016
À, có cách đơn giản hơn:
a/Ta đã có điều kiện n<1 mà n là số tự nhiên suy ra n = 0 , thay vào thỏa mãn.
b/ Ta cũng có điều kiện n < 5 mà n là số tự nhiên nên suy ra n = 0,1,2,3,4 thay vào xem giá trị nào thỏa mãn thì lấy
24 tháng 10 2016
a/ Để (16-3n) chia hết cho (n+4) thì thương \(A=\frac{16-3n}{n+4}\) nhận giá trị nguyên.
Xét \(\frac{16-3n}{n+4}=\frac{-3\left(n+4\right)+28}{n+4}=\frac{28}{n+4}-3\)
Từ đó suy ra A nhận giá trị nguyên khi (n+4) thuộc các ước của 28 .
Bạn liệt kê ra nhé :)
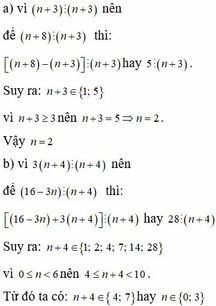
a) Để n + 9 chia hết cho n + 4 thì 9 và 4 phải cùng chia hết cho n và n \(\ne0\)
Ta có số n để 9 và 4 cùng chia hết cho n là 1.
Vậy n = 1.
b) Để 3n + 40 chia hết cho n + 4 thì 40 và 4 phải cùng chia hết cho n và n \(\ne0\)
Ta có các số n để 40 và 4 cùng chia hết cho n là 1 , 2 , 4 .
Vậy n có thể = 1, 2, 4.
c) Để 5n + 2 chia hết cho 2n + 9 thì 2 và 9 phải cùng chia hết cho n và n \(\ne0\)
Ta có số n để 2 và 9 cùng chia hết cho n là 1.
Vậy n = 1.
xl bn câu b) n có thể = 0 nữa nha