Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có abcd chia hết cho 3 và 5 nên
d phải là tận cùng bằng 5 hoặc 0
a+b+c+d phải chia hết cho 3
từ đó ta rút ra có 2 số chia hết cho 5 là 8765 và 3210 nhưng vì 8765 ko chia hết cho 3 nên
số cần tìm là 3210

a, Gọi ba số tự nhiên liên tiếp là: a; a+1; a+2 tổng của ba số này bằng: a+a+1+a+2 = 3a + 3 = 3(a+1) là một số chia hết cho 3.
b, Gọi bốn số tự nhiên liên tiếp là: a; a+1; a+2; a+3 tổng của bốn số này bằng: a+a+1+a+2+a+3 = 4a+6, là một số chia không hết cho 4 vì 4a ⋮ 4 và 6 không chia hết cho 4
c, Ta có: a b - b a = 10 a + b - 10 b + a = 9a - 9b = 9(a - b) với a > b
Mà 9(a - b) ⋮ 9 nên a b - b a ⋮ 9
d, Ta có: a b c d = 100 a b + c d = 99 a b + a b + c d
Mà 99 a b ⋮ 11 và a b + c d ⋮ 11 (đề bài), nên a b c d ⋮ 11

a) Ta có : \(x-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
...
b) Ta có : \(2x+1\inƯ\left(28\right)=\left\{\pm1;\pm2;\pm4;\pm7;\pm12;\pm28\right\}\)
Mà \(2x+1\)là số chẵn
\(\Rightarrow2x+1\in\left\{\pm1;\pm7\right\}\)
...
c) Ta có : \(x+15\)là bội của \(x+3\)
\(\Rightarrow x+15⋮x+3\)
\(\Rightarrow x+3+12⋮x+3\)
Vì \(x+3⋮x+3\)
\(\Rightarrow12⋮x+3\)
\(\Rightarrow x+3\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
...


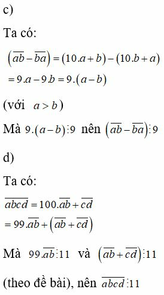
Ta có:
abcd chia hết cho 3 và 5 nên d phải là tận cùng bằng 5 hoặc 0
⇒a+b+c+d phải chia hết cho 3
từ đó ta rút ra có 2 số chia hết cho 5 là 8765 và 3210 nhưng vì 8765 không chia hết cho 3
⇒ số đó là 3210
Có 4 cách chia:
Cách chia bi nhiều túi nhất là cách 4,ta được 6 túi ,
Lần lượt chia đều bi đỏ vào 6 túi;
48:6= 8 (viên mỗi túi)
Chia đều bi xanh vào 6 túi;
30 :6=5 (viên mỗi túi)
Chia đều bi vàng vào 6 túi;
66:6=11 (viên mỗi túi)
Tổng cộng số viên bi trong mỗi túi ;
8+5+11=24 (viên mỗi túi)