Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 xét x=0 => A =0
xét x>0 thì \(A=\frac{1}{x-2+\frac{2}{\sqrt{x}}}\)
để A nguyên thì \(x-2+\frac{2}{\sqrt{x}}\inƯ\left(1\right)\)
=>cho \(x-2+\frac{2}{\sqrt{x}}\)bằng 1 và -1 rồi giải ra =>x=?
1,Ta có \(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ac}\)
=> \(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=2\)
\(a+2=a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\)
\(b+2=\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{a}\right)\)
\(c+2=\left(\sqrt{c}+\sqrt{b}\right)\left(\sqrt{c}+\sqrt{a}\right)\)
=> \(\frac{\sqrt{a}}{a+2}+\frac{\sqrt{b}}{b+2}+\frac{\sqrt{c}}{c+2}=\frac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}+\frac{\sqrt{b}}{\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{a}\right)}+...\)
=> \(\frac{\sqrt{a}}{a+2}+...=\frac{2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}=\frac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)
=> M=0
Vậy M=0

a) \(\sqrt{ }\)20 + 2\(\sqrt{ }\)45 - 3\(\sqrt{ }\)80 + \(\sqrt{ }\)125
= \(\sqrt{ }\)4.5 +2\(\sqrt{ }\)9.5 - 3\(\sqrt{16.5}\)
= 2\(\sqrt{5}\) + 6\(\sqrt{5}\) - 12\(\sqrt{5}\)
= -4\(\sqrt{5}\)
b) \(\dfrac{2\sqrt{3}+3\sqrt{2}}{\sqrt{3}+\sqrt{2}}\) - \(4\sqrt{\dfrac{3}{2}}\)- \(\dfrac{5}{1-\sqrt{6}}\)
= \(\dfrac{2\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\)- \(\sqrt{16.\dfrac{3}{2}}\) - \(\dfrac{5\left(1+\sqrt{6}\right)}{\left(1-\sqrt{6}\right)\left(1+\sqrt{6}\right)}\)
= 2 - \(\sqrt{24}\) - \(\dfrac{5\left(1+\sqrt{6}\right)}{1-6}\)
= 2 - \(\sqrt{4.6}\) + 1+\(\sqrt{ }\)6
= 2 - 2\(\sqrt{ }\)6 + 1+\(\sqrt{ }\)6
= 3 - \(\sqrt{ }\)6
c) (đề bài) với x khác 4...
= \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)- \(\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
= \(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-2\right)}\)- ....
= \(x-4\sqrt{x}+4\)/ \(\sqrt{x}\left(\sqrt{x}-2\right)\)
= (căn -2)2/ căn x(căn x -2)
= căn x-2/căn x

a: \(A=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\sqrt{a}-\sqrt{b}-\sqrt{a}-\sqrt{b}=-2\sqrt{b}\)
b: \(B=\dfrac{2\sqrt{x}-x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{-2x+\sqrt{x}-1}{\sqrt{x}-1}\cdot\dfrac{1}{x-1}\)
c: \(C=\dfrac{x-9-x+3\sqrt{x}}{x-9}:\left(\dfrac{3-\sqrt{x}}{\sqrt{x}-2}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}+\dfrac{x-9}{x+\sqrt{x}-6}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{x-9}:\dfrac{9-x+x-4\sqrt{x}+4+x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\cdot\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{x-4\sqrt{x}+4}\)
\(=\dfrac{3}{\sqrt{x}-2}\)
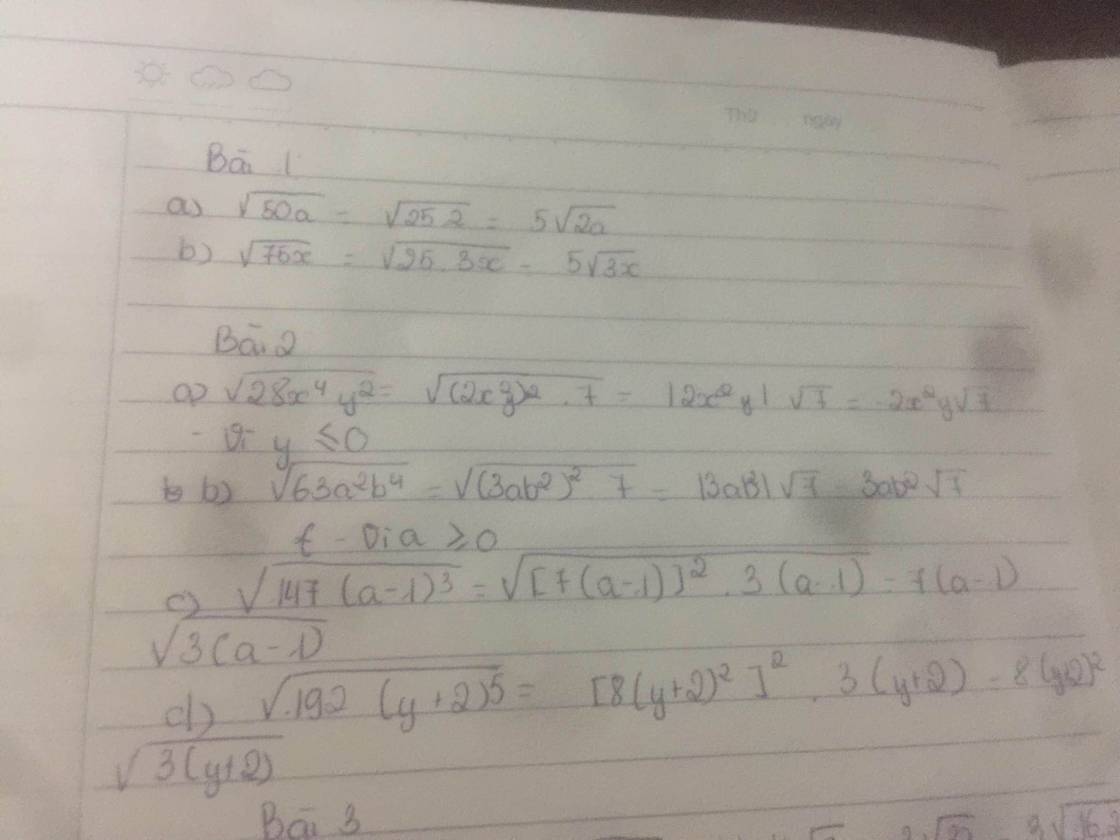
xem gi
co ban nho cua toi
may bi loi unikey thong cam nha moi nguoi
hihi
a) \(\sqrt[3]{x}< 2\Leftrightarrow\left(\sqrt[3]{x}\right)^3< 2^3\Leftrightarrow x< 8\)
b) \(\sqrt[3]{2x-1}>-3\Leftrightarrow\left(\sqrt[3]{2x-1}\right)^3>\left(-3\right)^3\Leftrightarrow2x-1>-27\Leftrightarrow2x>-26\Leftrightarrow x>-13\)
c) \(\sqrt[3]{2-3x}\le1\Leftrightarrow\left(\sqrt[3]{2-3x}\right)^3\le1\Leftrightarrow2-3x\le1\Leftrightarrow3x\ge1\Leftrightarrow x\ge\frac{1}{3}\)
d) \(\sqrt[3]{3-4x}\ge5\Leftrightarrow\left(\sqrt[3]{3-4x}\right)^3\ge5^3\Leftrightarrow3-4x\ge125\Leftrightarrow4x\le-122\Leftrightarrow x\le-\frac{61}{2}\)