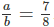Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đầu bài ta có:
\(\frac{a}{a-b}=8\cdot\frac{a}{b}\)
\(\Rightarrow\frac{a-b}{a}=\frac{b}{8\cdot a}\)
\(\Rightarrow1-\frac{b}{a}=\frac{b}{a}\cdot\frac{1}{8}\)
\(\Rightarrow1=\frac{b}{a}\cdot\frac{1}{8}+\frac{b}{a}\)
\(\Rightarrow\frac{b}{a}\cdot\frac{9}{8}=1\)
\(\Rightarrow1:\frac{a}{b}=1:\frac{9}{8}\)
\(\Rightarrow\frac{a}{b}=\frac{9}{8}\)
Thử lại: \(\frac{9}{8}\cdot8=9=\frac{9}{9-8}\) ( đúng với đề bài )
Vậy phân số a/b cần tìm là 9/8

Giải:
Ta có:
\(\dfrac{a}{b}=\dfrac{-8}{11}\left(1\right)\Leftrightarrow1-\dfrac{a}{b}=1-\dfrac{-8}{11}\)
Hay \(\dfrac{b-a}{b}=\dfrac{11+8}{11}=\dfrac{19}{11}\left(2\right)\)
Thay \(b-a=190\) vào \(\left(2\right)\) ta được:
\(\dfrac{190}{b}=\dfrac{19}{11}\Leftrightarrow190.11=19b\Leftrightarrow b=110\)
Thay \(b=110\) vào \(\left(1\right)\) ta được:
\(\dfrac{a}{110}=\dfrac{-8}{11}\Leftrightarrow11a=-8.110\Leftrightarrow a=-80\)
Vậy phân số \(\dfrac{a}{b}\) cần tìm là \(\dfrac{-80}{110}\)
Thay b - a = 190 vào (1) ta được:
Phân số a/b phải tìm là -80/110

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

Ta có:
Mà a = b + c nên
Từ (1), (2) suy ra:
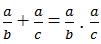

Ta có \(\dfrac{a}{b}=\dfrac{18}{27}=\dfrac{2}{3}\)
Mà \(ƯCLN\left(a,b\right)=13\)
\(\Rightarrow\dfrac{a}{b}\) sau khi rút gọn cho 13 sẽ bằng \(\dfrac{2}{3}\)
Vậy \(\dfrac{a}{b}=\dfrac{2.13}{3.13}=\dfrac{26}{39}\)
Trước hết ta đưa \(\dfrac{18}{27}\) về phân số tối giản. Ta có:\(\dfrac{18}{27}=\dfrac{2}{3}\)
\(\dfrac{2.13}{3.13}=\dfrac{26}{39}\)

Phân số (B) không là phân số tối giản (vì cả tử và mẫu vẫn chia hết được cho 7).![]()
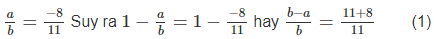
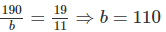
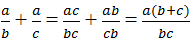
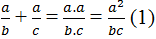
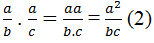
Từ = (a / b).8, suy ra:
= (a / b).8, suy ra:
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay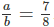
Từ = (a / b).8, suy ra:
= (a / b).8, suy ra:
ab = 8a(b – a)
ab = 8ab – 8a2
8a2 = 7ab
8a = 7b hay