T
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
13 tháng 10 2017
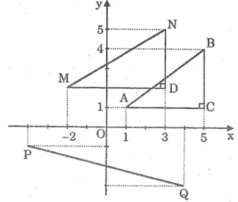
Ta có: M N 2 = M D 2 + N D 2 = 3 + 2 2 + 3 - 2 2 = 25 + 9 = 34
AB = 34 ≈ 5,83
PT
1
CM
25 tháng 7 2017
Ta có: A B 2 = A C 2 + B C 2 = 5 - 1 2 + 4 - 1 2 = 16 + 9 = 25
AB = 25 = 5
23 tháng 4 2023
PTHĐGĐ là:
x^2-2x-m+2=0
Δ=(-2)^2-4(-m+2)
=4+4m-8=4m-4
Để (P) tiếp xúc (d) thì 4m-4=0
=>m=1
=>x^2-2x+1=0
=>x=1
=>y=1
29 tháng 7 2023
1:
a: 
b: PTHĐGĐ là:
-1/4x^2-x-1=0
=>x^2+4x+4=0
=>(x+2)^2=0
=>x=-2
=>y=-1/4*(-2)^2=-1
2: 3x-y=5 và 2x+3y=18
=>9x-3y=15 và 2x+3y=18
=>11x=33 và 3x-y=5
=>x=3 và y=3*3-5=4
22 tháng 5 2021
Xét pt hoành độ gđ của (d) và (P) có:
\(x^2=2x+4m^2-8m+3\)
\(\Leftrightarrow x^2-2x-4m^2+8m-3=0\) (1)
\(\Delta=4-4\left(-4m^2+8m-3\right)\)\(=16m^2-32m+16=16\left(m-1\right)^2\)
Để (P) và (d) cắt nhau tại hai điểm pb khi pt (1) có hai nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow m\ne1\)
Có \(A\in\left(P\right)\Rightarrow y_1=x_1^2\)
\(B\in\left(P\right)\Rightarrow y_2=x_2^2\) , trong đó x1; x2 là hai nghiệm của pt (1)
Theo định lí viet có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-4m^2+8m-3\end{matrix}\right.\)
\(y_1+y_2=10\)
\(\Leftrightarrow x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(-4m^2+8m-3\right)=10\)
\(\Leftrightarrow8m^2-16m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)(tm)
Vậy...
30 tháng 4 2021
a) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{x^2}{2}=mx-m+2\)
\(\Leftrightarrow\dfrac{1}{2}x^2-mx+m-2=0\)
\(\Delta=\left(-m\right)^2-4\cdot\dfrac{1}{2}\cdot\left(m-2\right)=m^2-2m+4>0\forall m\)
Do đó: (P) và (d) luôn cắt nhau tại hai điểm phân biệt(Đpcm)
23 tháng 4 2023
PTHĐGĐ là:
x^2-2x-m+1=0
Δ=(-2)^2-4*1*(-m+1)
=4+4m-4=4m
Để (P) tiếp xúc (d) thì 4m=0
=>m=0
=>x^2-2x+1=0
=>x=1
=>y=1