TB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 11 2017
a2(b+c)2+5bc+b2(a+c)2+5ac≥4a29(b+c)2+4b29(a+c)2=49(a2(1−a)2+b2(1−b)2)(vì a+b+c=1)
a2(1−a)2−9a−24=(2−x)(3x−1)24(1−a)2≥0(vì )<a<1)
⇒a2(1−a)2≥9a−24
tương tự: b2(1−b)2≥9b−24
⇒P⩾49(9a−24+9b−24)−3(a+b)24=(a+b)−94−3(a+b)24.
đặt t=a+b(0<t<1)⇒P≥F(t)=−3t24+t−94(∗)
Xét hàm (∗) được: MinF(t)=F(23)=−19
⇒MinP=MinF(t)=−19.dấu "=" xảy ra khi a=b=c=13
9 tháng 10 2020
Câu 1:
\(a^3+a^2b-ab^2-b^3\)
\(=a^2\left(a+b\right)-b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-b^2\right)\)
\(=\left(a+b\right)\left(a-b\right)\left(a+b\right)\)
\(=\left(a+b\right)^2\left(a-b\right)\)
9 tháng 10 2020
Câu 2:
\(a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)\)
\(=a\left(b^3-c^3\right)+bc^3-a^3b+a^3c-b^3c\)
\(=a\left(b-c\right)\left(b^2+bc+c^2\right)-a^3\left(b-c\right)-bc\left(b-c\right)\left(b+c\right)\)
\(=\left(b-c\right)\left(ab^2+abc+c^2a-a^3-b^2c-bc^2\right)\)
\(=\left(b-c\right)\left[a\left(c-a\right)\left(c+a\right)-b^2\left(c-a\right)-bc\left(c-a\right)\right]\)
\(=\left(b-c\right)\left(c-a\right)\left(ca+a^2-b^2-bc\right)\)
\(=\left(b-c\right)\left(c-a\right)\left[\left(a-b\right)\left(a+b\right)+c\left(a-b\right)\right]\)
\(=\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)\)
2 tháng 3 2017
\(P=\frac{a^3}{a^2+2b^2}+\frac{b^3}{b^2+2a^2}\)
\(\Leftrightarrow P=a-\frac{2ab^2}{a^2+2b^2}+b-\frac{2a^2b}{b^2+2a^2}\)
Áp dụng bất đẳng thức Cauchy cho 2 bộ số thực không âm
\(\Rightarrow\hept{\begin{cases}a^2+2b^2\ge2\sqrt{2a^2b^2}=2ab\sqrt{2}\\b^2+2a^2\ge2\sqrt{2a^2b^2}=2ab\sqrt{2}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\frac{2ab^2}{a^2+2b^2}\le\frac{2ab^2}{2ab\sqrt{2}}=\frac{b}{\sqrt{2}}\\\frac{2a^2b}{b^2+2a^2}\le\frac{2a^2b}{2ab\sqrt{2}}=\frac{a}{\sqrt{2}}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a-\frac{2ab^2}{a^2+2b^2}\ge a-\frac{b}{\sqrt{2}}\\b-\frac{2a^2b}{b^2+2a^2}\ge b-\frac{a}{\sqrt{2}}\end{cases}}\)
\(\Rightarrow a-\frac{2ab^2}{a^2+2b^2}+b-\frac{2a^2b}{b^2+2a^2}\ge a+b-\left(\frac{a+b}{\sqrt{2}}\right)\)
\(\Rightarrow a-\frac{2ab^2}{a^2+2b^2}+b-\frac{2a^2b}{b^2+2a^2}\ge\frac{\left(2-\sqrt{2}\right)\left(a+b\right)}{2}\)
Ta có \(\sqrt{\left(a+2\right)\left(b+2\right)}\ge9\)
Áp dụng bất đẳng thức Cauchy cho 2 bộ số thực không âm
\(\Rightarrow9\le\sqrt{\left(a+2\right)\left(b+2\right)}\le\frac{a+b+4}{2}\)
\(\Rightarrow9\le\frac{a+b+4}{2}\)
\(\Rightarrow a+b\ge14\)
\(\Rightarrow\frac{\left(2-\sqrt{2}\right)\left(a+b\right)}{2}\ge14-7\sqrt{2}\)
\(\Rightarrow a-\frac{2ab^2}{a^2+2b^2}+b-\frac{2a^2b}{b^2+2a^2}\ge14-7\sqrt{2}\)
\(\Rightarrow P\ge14-7\sqrt{2}\)
Vậy GTNN của \(P=14-7\sqrt{2}\)
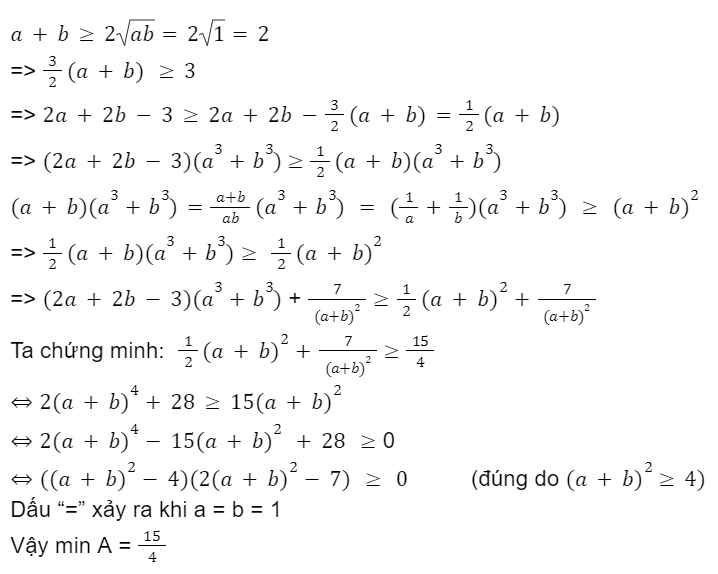
đề này thiếu à