Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A (x;y) là giao điểm của d, d1 và d2. tọa độ giao điểm điểm của A là nghiệm của hpt : d và d1. ( giải được nghiệm x, y sẽ chứa tham số m ), nếu có m ở mẫu thì tìm đk của xác định của m nhé
sau đó thay tọa độ A tìm được vào d2 sẽ tìm ra m .

Lời giải:
Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$
Vậy giao điểm của 2 ĐT trên là $(-1,0)$
Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$
$\Leftrightarrow m=-1$

Giả sử hai đường thẳng ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại điểm B(x, y).
Vì điểm B nằm trên trục Ox nên y = 0 ⇒ B( x, 0).
Khi đó điểm B(x; 0) là nghiệm của hệ phương trình: 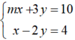
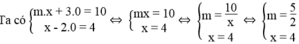
Vậy khi m = 5/2 thì ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại một điểm trên trục Ox.
Phương trình đường thẳng (d1):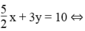 5x + 6y = 20
5x + 6y = 20
*Vẽ ( d 1 ): Cho x = 0 thì y = 10/3 ⇒ (0; 10/3 )
Cho y = 0 thì x = 4 ⇒ (4; 0)
*Vẽ ( d 2 ): x - 2y = 4. Cho x = 0 thì y = -2 ⇒ (0; -2)
Cho y = 0 thì x = 4 ⇒ (4; 0)
Đồ thị:
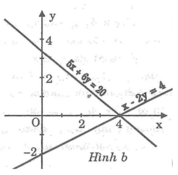

b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2

+) Thay tọa độ điểm I vào phương trình d1 ta được:
m.(−5) – 2(3n + 2).2 = 18 ⇔ −5m – 12n − 8 = 18 ⇔ 5m + 12n = −26
+) Thay tọa độ điểm I vào phương trình d 2 ta được:
(3m – 1). (−5) + 2n.2 = −37 ⇔ −15m + 5 + 4n = −37 ⇔ 15m – 4n = 42
Suy ra hệ phương trình
5 m + 12 n = − 26 15 m − 4 n = 42 ⇔ 5 m + 12 n = − 26 n = 15 m − 42 4 ⇔ n = 15 m − 42 4 5 m + 12. 15 m − 42 4 = − 26 ⇔ n = 15 m − 42 4 5 m + 3 15 m − 42 = − 26
⇔ n = 15 m − 42 4 50 m − 126 = − 26 ⇔ m = 2 n = − 3
Vậy m = 2; n = −3
Đáp án: C

\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)
Ta có (d1) : \(mx+y=1\)
=> \(y=1-mx\)
Ta có (d2) : \(x-my=m+6\)
=> \(y=\frac{x-m-6}{m}\)( I )
- Xét phương trình hoành độ giao điểm :
\(1-mx=\frac{x-m-6}{m}\)
=> \(m-m^2x=x-m-6\)
=> \(-m^2x-x=-m-6-m\)
=> \(x\left(-m^2-1\right)=-2m-6\)
=> \(x=\frac{2m+6}{m^2+1}\)
- Thay \(x=\frac{2m+6}{m^2+1}\) vào phương trình ( I ) ta được :
\(y=\frac{\frac{2m-6}{m^2+1}-m-6}{m}\)
- Thay \(y=\frac{\frac{2m-6}{m^2+1}-m-6}{m}\); \(x=\frac{2m+6}{m^2+1}\) vào đường thẳng (d) ta được :
\(\frac{2m+6}{m^2+1}+\frac{2\left(\frac{2m-6}{m^2+1}-m-6\right)}{m}=8\)
=> \(\frac{m\left(2m+6\right)}{m\left(m^2+1\right)}+\frac{2\left(\frac{2m-6}{m^2+1}-m-6\right)\left(m^2+1\right)}{m\left(m^2+1\right)}=8\)
=> \(\frac{m\left(2m+6\right)}{m\left(m^2+1\right)}+\frac{\frac{\left(4m-12\right)\left(m^1+1\right)}{m^2+1}-2m\left(m^2+1\right)-12\left(m^2+1\right)}{m\left(m^2+1\right)}=8\)
=> \(\left(4m-12\right)-2m\left(m^2+1\right)-12\left(m^2+1\right)+m\left(2m+6\right)=8m\left(m^2+1\right)\)
=> \(4m-12-2m^3-2m-12m^2-12+2m^2+6m=8m^3+8m\)
=> \(10m^3+10m^2+24=0\)
=> \(m^3+m^2+\frac{12}{5}=0\)
=> \(m\approx-1,76\)