Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Có. Ví dụ: (3 - √3) và (2 + √3) là hai số vô tỉ dương, nhưng (3 - √3) + (2 + √3) = 5 là một số hữu tỉ.

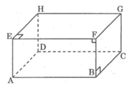
Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a) sai.

\(Q=\left(a^2b^2+a^2+b^2+1\right)\left(c^2+1\right)=\)
\(=a^2b^2c^2+a^2b^2+a^2c^2+a^2+b^2c^2+b^2+c^2+1=\)
\(=a^2b^2c^2+\left(a^2b^2+b^2c^2+a^2c^2\right)+\left(a^2+b^2+c^2\right)+1\) (1)
Ta có
\(\left(ab+bc+ac\right)^2=a^2b^2+b^2c^2+a^2c^2+2ab^2c+2abc^2+2a^2bc=\)
\(=a^2b^2+b^2c^2+a^2c^2+2abc\left(a+b+c\right)=1\)
\(\Rightarrow a^2b^2+b^2c^2+a^2c^2=1-2abc\left(a+b+c\right)\) (2)
Ta có
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ac\right)=\)
\(=a^2+b^2+c^2+2\)
\(\Rightarrow a^2+b^2+c^2=\left(a+b+c\right)^2-2\) (3)
Thay (2) và (3) vào (1)
\(Q=a^2b^2c^2+1-2abc\left(a+b+c\right)+\left(a+b+c\right)^2-2+1=\)
\(=\left(abc\right)^2-2abc\left(a+b+c\right)+\left(a+b+c\right)^2=\)
\(=\left[abc-\left(a+b+c\right)\right]^2\)