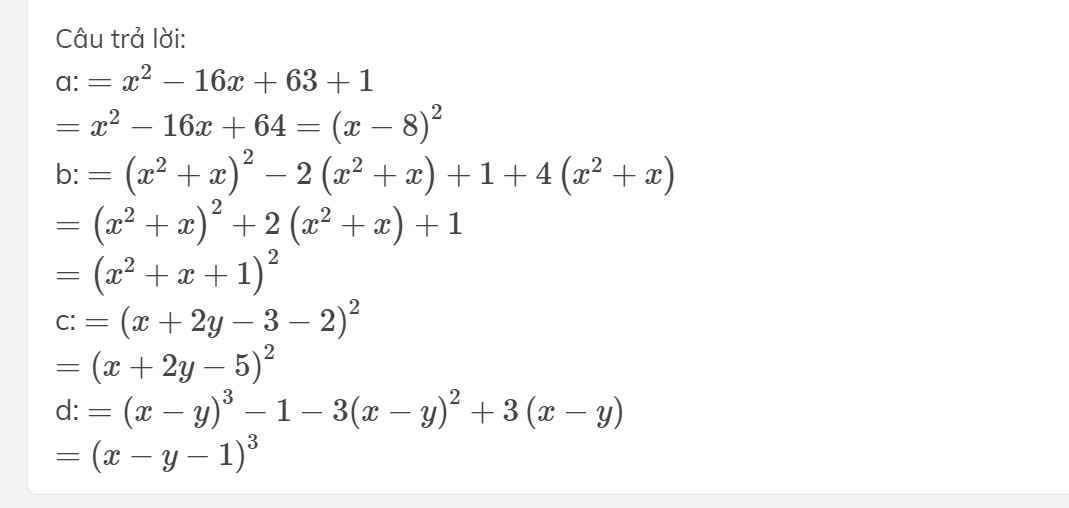Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xin câu a :3
a) (x + y + 1)2 = 3(x2 + y2) + 1
<=> x2 + y2 + 1 + 2xy + 2x + 2y = 3x2 + 3y2 + 1
<=> 2x2 + 2y2 - 2xy - 2x - 2y = 0
<=> (x2 - 2xy + y2) + (x2 - 2x + 1) + (y2 - 2y + 1) = 2
<=> (x - y)2 + (x - 1)2 + (y - 1)2 = 2
Vì 2 = 02 + 12 + 12 nên ta có các TH sau:
TH1:
\(\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-1\right)^2=1\\\left(y-1\right)^2=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=y=2\\x=y=0\end{matrix}\right.\)
TH2:
\(\left\{{}\begin{matrix}\left(x-y\right)^2=1\\\left(x-1\right)^2=0\\\left(y-1\right)^2=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1;y=0\\x=1;y=2\end{matrix}\right.\)
TH3:
\(\left\{{}\begin{matrix}\left(x-y\right)^2=1\\\left(x-1\right)^2=1\\\left(y-1\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2;y=1\\x=0;y=1\end{matrix}\right.\)
Vậy ...
a) ta có : \(\left(x+y+1\right)^2=3\left(x^2+y^2\right)+1\)
\(\Leftrightarrow x^2+y^2+1+2xy+2y+2x=3x^2+3y^2+1\)
\(\Leftrightarrow-\left(x-1\right)^2-\left(y-1\right)^2=\left(x-y\right)^2-2\le0\)
\(\Leftrightarrow-\sqrt{2}\le x-y\le\sqrt{2}\) --> ...
b) \(\left(2x-y-2\right)^2=7\left(x-2y-y^2-1\right)\)
\(\Leftrightarrow4x^2+y^2+4-4xy+4y-4x=7x-14y-7y^2-7\)
\(\Leftrightarrow2x^2-4xy+2y^2+2x^2-11x+\dfrac{121}{16}+6y^2+18y+\dfrac{9}{4}=\dfrac{-19}{16}\left(vl\right)\)
câu c tương tự .

\(M=4x\left(x+y+z\right)\left(x^2+xz+yx+yz\right)+\left(yz\right)^2\)
\(M=4\left(x^2+xy+zx\right)\left(x^2+yz+zx+xy\right)+\left(yz\right)^2\)
\(M=4\left(x^2+xy+zx\right)\left\{\left(x^2+yz+zx\right)+xy\right\}+\left(yz^2\right)\)
\(M=4\left(x^2+xy+zx\right)^2+4\left(x^2+yz+zx\right)\left(yz\right)+\left(yz\right)^2\) ( hằng đẳng thức )
\(M=\left\{2\left(x^2+xy+zx\right)\right\}^2+2.2\left(x^2+xy+zx\right)\left(yz\right)+\left(yz\right)^2\)
\(M=\left(2\left(x^2+xy+zx\right)+\left(yz\right)\right)^2\)
\(M=\left(2x^2+2xy+zx+yz\right)^2\)
\(M=4x\left(x+y\right)\left(x+y+z\right)\left(x+z\right)+y^2z^2\)
\(=2x\left(x+y+z\right)2\left(x+y\right)\left(x+z\right)+y^2z^2\)
\(=\left(2x^2+2xy+2xz\right)\left(2x^2+2xy+2xz+2yz\right)+y^2z^2\)
Đặt \(2x^2+2xy+2xz+yz=a\)
\(M=\left(a-yz\right)\left(a+yz\right)+y^2z^2\)
\(=a^2-y^2z^2+y^2z^2\)
\(=a^2\)
Mà \(x;y;z\in N\Rightarrow a\in N\)
=> M là số chính phương

a) Ta có: \(2018^n-1964^n⋮3\)
\(2032^n-1984^n⋮3\)
nên An chia hết cho 3
Mà \(2018^n-1984^n⋮17\)
\(2032^n-1964^n⋮17\)
nên An chia hết cho 17
Vậy A chia hết cho 51
b) Ta có: An đồng dư 3^n +2^n-2.4^n (mod5)
và An đồng dư 2^n + 7^n -2^n-4^n (mod9)
Vậy An chia hết cho 45 khi n có dạng 12k

\(B=x^2-6x+y^2-2y+12=\left(x^2-6x+9\right)\left(y^2-2y+1\right)+2\)
\(B=\left(x-3\right)^2+\left(y-1\right)^2+2\text{ }\)
Ta thấy B lớn hơn hoặc bằng 2 suy ra GTNN của B là 2
Dấu = xảy ra khi x=3; y=1
\(C=2x^2-6x=\left(2x^2-6x+4,5\right)-4,5=2\left(x^2-3x+2,25\right)-4,5\)
\(C=2\left(x-1,5\right)^2-4,5\)
Ta thấy C luôn luôn lớn hơn hoặc bằng -4,5 nên GTNN của C là -4,5
Dấu = xảy ra khi x=1,5
Tối mình full cho còn giờ mình đi đá bóng đây
1) \(D=\frac{2016}{-4x^2+4x-5}\). Để D đạt giá trị nhỏ nhất suy ra \(-4x^2+4x-5\)đạt giá trị lớn nhất.
Ta có \(-4x^2+4x-5=-4x^2+4x-1-4=\left(-4x^2+4x-1\right)-4\)
\(-4\left(x^2-x+\frac{1}{4}\right)-4=-4\left(x-\frac{1}{2}\right)^2-4\).
Ta Thấy:\(-4\left(x-\frac{1}{2}\right)^2\) bé hơn hoặc bằng 0 nên \(-4\left(x-\frac{1}{2}\right)^2-4\)bé hơn hoặc bằng -4
nên ..... bạn tự kết luận

a)\(=\left(x^2-7x-9x+63\right)+1\)
\(=x^2-7x-9x+63+1\)
=\(x^2-16x+64\)
\(=\left(x-8\right)^2\)
a: \(=x^2-16x+63+1\)
\(=x^2-16x+64=\left(x-8\right)^2\)
b: \(=\left(x^2+x\right)^2-2\left(x^2+x\right)+1+4\left(x^2+x\right)\)
\(=\left(x^2+x\right)^2+2\left(x^2+x\right)+1\)
\(=\left(x^2+x+1\right)^2\)
c: \(=\left(x+2y-3-2\right)^2\)
\(=\left(x+2y-5\right)^2\)
d: \(=\left(x-y\right)^3-1-3\left(x-y\right)^2+3\left(x-y\right)\)
\(=\left(x-y-1\right)^3\)