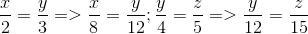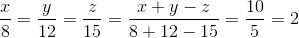Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{12}\Leftrightarrow\dfrac{-x}{-8}=\dfrac{y}{5}=\dfrac{z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{-x}{-8}=\dfrac{y}{5}=\dfrac{z}{12}=\dfrac{-x+y+z}{-8+5+12}=\dfrac{60}{9}=\dfrac{20}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{20}{3}.8=\dfrac{160}{3}\\y=\dfrac{20}{3}.5=\dfrac{100}{3}\\z=\dfrac{20}{3}.12=80\end{matrix}\right.\)
b) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Leftrightarrow\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x+2y-3z}{2+6-12}=\dfrac{-20}{-4}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5.2=10\\y=5.3=15\\z=5.4=20\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}4x=3y\\7y=5z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{4}\\\dfrac{y}{5}=\dfrac{z}{7}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=\dfrac{y}{20}\\\dfrac{y}{20}=\dfrac{z}{28}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{x-y+z}{15-20+28}=\dfrac{-46}{23}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2.15=-30\\y=-2.20=-40\\z=-2.28=-56\end{matrix}\right.\)

a,3x=2y;7y=5z
=>\(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta co:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x-y+z}{10-15+21}=\dfrac{32}{16}=2\\ \Rightarrow x=2.10=20\\ y=2.15=30\\ z=2.21=42\)
Các câu sau tương tự
b,\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\),\(\dfrac{y}{3}\)=\(\dfrac{z}{5}\) và 2x-3y+z=6
Từ đề bài ta có:
\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)\(\Rightarrow\)\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)(1)
\(\dfrac{y}{3}\)=\(\dfrac{z}{5}\)\(\Rightarrow\)\(\dfrac{y}{12}\)=\(\dfrac{z}{20}\)(2)
từ (1) và (2)\(\Rightarrow\)\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)=\(\dfrac{z}{20}\)\(\Rightarrow\)\(\dfrac{2x}{18}\)=\(\dfrac{3y}{36}\)=\(\dfrac{z}{20}\)
Áp dụng t/c dãy tỉ số bằng nhau,ta có:
\(\dfrac{2x}{18}\)=\(\dfrac{3y}{36}\)=\(\dfrac{z}{20}\)=\(\dfrac{2x-3y+z}{18-36+20}\)=\(\dfrac{6}{2}\)=3
\(\Rightarrow\)x=3.9=27
y=3.12=36
z=3.20=60
Vậy.....
chúc bạn học tốt,nhớ tick cho mình nha![]()

b: Ta có: x/y=7/9
nên x/7=y/9
=>x/49=y/63
Ta có: y/z=7/3
nên y/7=z/3
=>y/63=z/27
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{49}=\dfrac{y}{63}=\dfrac{z}{27}=\dfrac{x-y+z}{49-63+27}=\dfrac{-15}{13}\)
Do đó: x=-735/13; y=-945/13; z=-405/13
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{20}=\dfrac{z}{32}=\dfrac{2x+5y-2z}{2\cdot7+5\cdot20-2\cdot32}=\dfrac{100}{50}=2\)
Do đó: x=14; y=40; z=64
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x-y-z}{8-5-2}=3\)
Do đó: x=24; y=15; z=6

a)Vì \(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)nên \(\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{x}{28}\).
Áp dụng t/c dãy tỉ số = nhau, ta có :
\(\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{z}{28}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{186}{62}=3\)
⇒2x = 3.30 = 90 ⇒ x = 45
3y = 3.60 = 180 ⇒ y = 60
z = 3.28 = 84
Ý b) có gì đó sai sai ?
c)Ta có :
\(2x=3y=5z\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dãy tỉ số = nhau, ta có :
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y-z}{15+10-6}=\dfrac{95}{19}=5\)
⇒x = 5.15 = 75
y = 5.10 = 50
z = 5.6 = 30
d)Ta có :
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=k\left(k\in Z\right)\)
⇒ x = 2k ; y = 3k ; z = 5k
⇒ xyz = 2k.3k.5k = 30k3 = 810
⇒ k = 3 Vậy x = 3.2 = 6; y = 3.3 = 9; z = 3.5 = 15
1/ a, Ta có :
\(x-2y+3z=35\)
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{3-8+15}=\dfrac{35}{10}=\dfrac{7}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{7}{2}\Leftrightarrow x=\dfrac{21}{2}\\\dfrac{x}{4}=\dfrac{7}{2}\Leftrightarrow y=14\\\dfrac{z}{5}=\dfrac{7}{2}\Leftrightarrow z=\dfrac{35}{2}\end{matrix}\right.\)
Vậy ..

Bài 1:
a: \(\Leftrightarrow\dfrac{x+2}{2}=x-5\)
=>2x-10=x+2
=>x=12
b: \(\Leftrightarrow\left(x+2\right)^2=100\)
=>x+2=10 hoặc x+2=-10
=>x=-12 hoặc x=8
c: \(\Leftrightarrow\left(2x-5\right)^3=27\)
=>2x-5=3
=>2x=8
=>x=4

Ta có \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{2.4}=\dfrac{y}{3.4}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\)
\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{4.3}=\dfrac{z}{3.5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\)
Do đó \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}và\) \(x+y-z=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Với\(\dfrac{x}{8}=2\Rightarrow x=16\)
\(\dfrac{y}{12}=2\Rightarrow y=24\)
\(\dfrac{z}{15}=2\Rightarrow z=30\)
Vậy x=16, y=24 và z=30

a)vì\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)=\(\dfrac{z}{5}\)=>\(\dfrac{2x}{6}\)=\(\dfrac{3y}{12}\)=\(\dfrac{5z}{25}\)và 2x+3y+5z=86
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\dfrac{2x}{6}\)=\(\dfrac{3y}{12}\)=\(\dfrac{5z}{25}\)=\(\dfrac{2x+3y+5z}{6+12+25}\)\(\dfrac{86}{43}\)=2
vì\(\dfrac{2x}{6}\)=2=>2x=2.6=12=>x=12:2=6
\(\dfrac{3y}{12}\)=2=>3y=12.2=24=>y=24:3=8
\(\dfrac{5z}{25}\)=2=>5z=25.2=50=>z=50:5=10
vậy x=6,y=8,z=10
vì\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)=>\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)(1)
\(\dfrac{y}{6}\)=\(\dfrac{z}{8}\)=>\(\dfrac{y}{12}\)=\(\dfrac{z}{16}\)(2)
từ (1)(2)=>\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)=\(\dfrac{z}{16}\)=>\(\dfrac{3x}{27}\)=\(\dfrac{2y}{24}\)=\(\dfrac{z}{16}\)và 3x-2y-z=13
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\dfrac{3x}{27}\)=\(\dfrac{2y}{24}\)=\(\dfrac{z}{16}\)=\(\dfrac{3x-2y-z}{27-24-16}\)=\(\dfrac{13}{-13}\)=-1
vì\(\dfrac{3x}{27}\)=-1=>3x=-1.27=-27=>x=-27x;3=-9
\(\dfrac{2y}{24}\)=-1=>2y=-1.24=-24=>y=-24:2=-12
\(\dfrac{z}{16}\)=-1=>z=-1.16=-16
vậy...