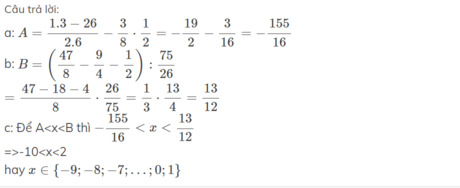BH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BN
1
NT
0
NT
4
10 tháng 1 2018
Ta có:
\(b=\frac{31+9a}{8}\) thê vô cái còn lại được
\(\frac{11}{7}< \frac{a}{\frac{31+9a}{8}}< \frac{23}{29}\)
\(\Leftrightarrow\frac{11}{7}< \frac{8a}{31+9a}< \frac{23}{29}\)
\(\Leftrightarrow\hept{\begin{cases}56a>341+99a\\232a< 713+207a\end{cases}}\)
\(\Leftrightarrow28< a< -7\)
Không tồn tại a,b tự nhiên thỏa bài toán
10 tháng 1 2018
tớ xin lỗi đề là 11\(\frac{11}{17}< \frac{a}{b}< \frac{23}{29}\)
DA
1
23 tháng 4 2017
Giải:
Theo đề bài ta có:
\(8b-9a=31\Rightarrow b=\dfrac{31+9a}{8}\)
\(=\dfrac{32-1+8a+a}{8}=\left[\left(4+a\right)+\dfrac{a-1}{8}\right]\) \(\in N\)
\(\Rightarrow\dfrac{a-1}{8}\in N\Leftrightarrow\left(a-1\right)⋮8\Rightarrow a=8k+1\left(k\in N\right)\)
Khi đó: \(b=\dfrac{31+9\left(8k+1\right)}{8}=9k+5\)
\(\Rightarrow\dfrac{11}{17}< \dfrac{8k+1}{9k+5}< \dfrac{23}{29}\)
\(\Rightarrow11\left(9k+5\right)< 17\left(8k+1\right)\Rightarrow37k>38\) \(\Rightarrow k>1\left(1\right)\)
Và \(29\left(8k+1\right)< 23\left(9k+5\right)\Rightarrow25k< 86\) \(\Rightarrow k< 4\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow1< k< 4\Leftrightarrow k\in\left\{2;3\right\}\)
Ta xét 2 trường hợp:
Trường hợp 1: Nếu \(k=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=8k+1\\b=9k+5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=8.2+1\\b=9.2+5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=17\\b=23\end{matrix}\right.\)
Trường hợp 2: Nếu \(k=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=8k+1\\b=9k+5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=8.3+1\\b=9.3+5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=25\\b=32\end{matrix}\right.\)
Vậy \(\left(a,b\right)=\left(17;23\right);\left(25;32\right)\)
ML
23 tháng 5 2016
2.P=\(\frac{3-a}{a+10}\)
a, để P>0
TH1 3-a>0 và a+10 >0
=> a<3 và a> -10
=> -10<a<3
TH2 3-a<0 và a+10<0
=> a>3 và a<-10(vô lý)
Vậy để P>0 thì -10<a<3
b.để P<0
TH1 3-a<0 và a+10>0
a>3 và a>-10
Vậy a>3
TH2 3-a>0 và a+10<0
=> a<3 và a<-10
Vậy a<-10
vậy để P<0 thì a >3 hoặc a<-10
ML
23 tháng 5 2016
bài 3.
a.\(\frac{7}{3}\)<x<\(\frac{17}{2}\)=>\(\frac{14}{6}\)<x<\(\frac{51}{6}\)
Vậy x=\(\left\{\frac{15}{6};\frac{16}{6};\frac{17}{6};..........;\frac{50}{6}\right\}\)
b.\(\frac{-3}{2}\)<y<2=>\(\frac{-3}{2}\)<y<\(\frac{4}{2}\)
Vậy y=\(\left\{\frac{-2}{2};\frac{-1}{2};\frac{0}{2};\frac{1}{2};\frac{2}{2};\frac{3}{2}\right\}\)
c.\(\frac{-17}{3}\)<z<\(\frac{-3}{2}\)=>\(\frac{-34}{6}\)<z<\(\frac{-9}{6}\)
Vậy z=\(\left\{\frac{-33}{6};\frac{-32}{6};\frac{-31}{6};.........\frac{-10}{6}\right\}\)
2 tháng 2 2022
a: \(A=\dfrac{1.3-26}{2.6}-\dfrac{3}{8}\cdot\dfrac{1}{2}=-\dfrac{19}{2}-\dfrac{3}{16}=-\dfrac{155}{16}\)
b: \(B=\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}\)
\(=\dfrac{47-18-4}{8}\cdot\dfrac{26}{75}=\dfrac{1}{3}\cdot\dfrac{13}{4}=\dfrac{13}{12}\)
c: Để A<x<B thì \(-\dfrac{155}{16}< x< \dfrac{13}{12}\)
=>-10<x<2
hay \(x\in\left\{-9;-8;-7;...;0;1\right\}\)