
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = \(\dfrac{1}{2}\).BG. AC = \(\dfrac{1}{2}\) 19.48 = 456 (mm2)
SAHE = 1212 AH. HE =\(\dfrac{1}{2}\)8.16 = 64 (mm2)
SDKC = \(\dfrac{1}{2}\) KC.KD = \(\dfrac{1}{2}\)22.23 = 253(mm2)
SHKDE = (HE+KD).HK2(HE+KD).HK2 = (16+23).182(16+23).182= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = 1/2.BG. AC = 1/2. 19.48 = 456 (mm2)
SAHE = 1/2 AH. HE = 1/2. 8.16 = 64 (mm2)
SDKC = 1/2 KC.KD = 1/2. 22.23 = 253(mm2)
SHKDE = (HE + KD).HK / 2 = (16 + 23).18 / 2= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)

A B E D H C
(Hình ảnh chỉ mang tính chất minh họa )
Giải:
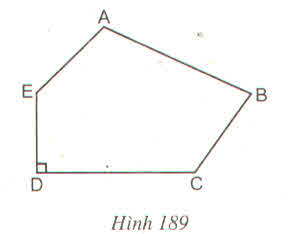
Chia thành tam giác AEB và tứ giác EDCB
kẽ AH\(\perp EB\left(H\in EB\right)\)
Ta đo được: ED=1,5 (cm) , EB=4(cm) , CD=3(cm) , AH= 1,2(cm)
SAEB=\(\dfrac{AH.EB}{2}=\dfrac{1,2.4}{2}=2,4\left(cm^2\right)\)
SEBCD=\(\dfrac{\left(EB+DC\right).ED}{2}=\dfrac{\left(4+3\right).1,5}{2}=5,25\left(cm^2\right)\)
=> SABCDE= SAEB+SEBCD=2,4 + 5,25=7,65(cm2)


a: \(\left(\dfrac{x+2}{x+1}-\dfrac{2x}{x-1}\right)\cdot\dfrac{3x+3}{x}+\dfrac{4x^2+x+7}{x^2-x}\)
\(=\dfrac{x^2+x-2-2x^2-2x}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{3\left(x+1\right)}{x}+\dfrac{4x^2+x+7}{x\left(x-1\right)}\)
\(=\dfrac{-x^2-x-2}{x-1}\cdot\dfrac{3}{x}+\dfrac{4x^2+x+7}{x\left(x-1\right)}\)
\(=\dfrac{-3x^2-3x-6+4x^2+x+7}{x\left(x-1\right)}=\dfrac{x^2-2x+1}{x\left(x-1\right)}=\dfrac{x-1}{x}\)

Chia đám đất ABCDE thành hình thang ABCE và tam giác ECD. Cần vẽ đường cao CH của hình thang và đường cao DK của tam giác. Thực hiện các phép đo chính xác đến mm ta được AB = 30mm, CE = 26mm, CH = 13mm, DK = 7mm.
Nên SABCE = \(\dfrac{\text{(AB+EC).CH}}{2}\) = \(\dfrac{\text{(30+26).13 }}{2}\)=364 (mm2)
SECD = \(\dfrac{1}{2}\) EC. DK = \(\dfrac{1}{2}\)267= 91 (mm2)
Do đó SABCDE = SABCE + SECD = 364 + 91 = 455 (mm2)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên diện tích đám đất là:
S = 455. 5000 = 2275000 (mm2) = 2,275 (m2)

Câu 4:
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(A=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Để A=-3 thì x-1=-6
hay x=-5(loại)

Điều kiện:
\(x-1\ne0\Rightarrow x\ne1\)
\(x^3+x\ne0\Leftrightarrow x\ne0\)
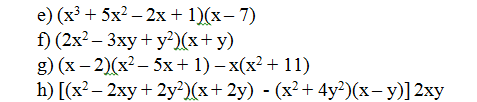




 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk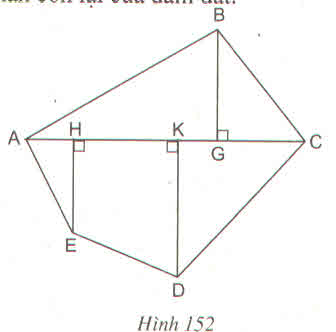






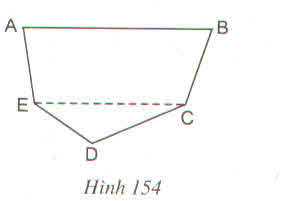


e: Ta có: \(\left(x-7\right)\left(x^3+5x^2-2x+1\right)\)
\(=x^4+5x^3-2x^2+x-7x^3-35x^2+14x-7\)
\(=x^4-2x^3-37x^2+15x-7\)
f: Ta có: \(\left(x+y\right)\left(2x^2-3xy+y^2\right)\)
\(=2x^3-3x^2y+xy^2+2x^2y-3xy^2+y^3\)
\(=2x^3-x^2y-2xy^2+y^3\)
g: Ta có: \(\left(x-2\right)\left(x^2-5x+1\right)-x\left(x^2+11\right)\)
\(=x^3-5x^2+x-2x^2+10x-2-x^3-11x\)
\(=-7x^2-2\)