
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=\dfrac{-3}{\left(x-2\right)^2}\)
d. Phương trình hoành độ giao điểm
\(\dfrac{x+1}{x-2}=x-\dfrac{1}{2}\Leftrightarrow2x^2-7x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Tại \(x=0\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{3}{4}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Pttt: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)
Tại \(x=\dfrac{7}{2}\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{4}{3}\\y=3\end{matrix}\right.\) tiếp tuyến: \(y=-\dfrac{4}{3}\left(x-\dfrac{7}{2}\right)+3\)
e.
Tam giác ABC là tam giác nào nhỉ? Có lẽ đó là tam giác OAB?
g.
Giao điểm (C) với Ox có tọa độ \(\left(-1;0\right)\)
\(\Rightarrow y'\left(-1\right)=-\dfrac{1}{3}\)
Phương trình tiếp tuyến:
\(y=-\dfrac{1}{3}\left(x+1\right)\)
h.
Giao điểm (C) với Oy có tọa độ \(\left(0;-\dfrac{1}{2}\right)\)
Chính là trường hợp đầu của câu d, phương trình: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)


Do tứ diện OABC có OA, OB, OC đôi một vuông góc nên H là trực tâm của tam giác ABC khi và chỉ khi H là hình chiếu của O trên mặt phẳng (P).
Vậy mặt phẳng (P) đi qua H(1;2;1) và nhận vecto \(\overrightarrow{OH}=\left(1;2;1\right)\) làm vecto pháp tuyến suy ra (P) có phương trình :
\(1.\left(x-1\right)+2\left(y-2\right)+1\left(z-1\right)=0\)
hay \(x+2y+z-6=0\)


a) Xét tam giác vuông $MBO$ vuông tại $B$ có đường cao $BH$:
\(\frac{1}{BH^2}=\frac{1}{MB^2}+\frac{1}{BO^2}=\frac{1}{BO^2-HO^2}\)\(\Rightarrow \frac{1}{MB^2}=\frac{1}{27}-\frac{1}{36}=\frac{1}{108}\Rightarrow MB=6\sqrt{3} (\text{cm})\)
b) Thấy rằng $BC$ là trung trực của $AO$ và $AO$ cũng là trung trực của $BC$ nên $BA=BO=OC=AC$
Mặt khác \(\cos(\widehat{BOH})=\frac{1}{2}\) nên \(\cos (\widehat{BOC})\neq 90^0\)
Do đó $OBAC$ là hình thoi
c) Vì $OA$ là trung trực của $BC$ nên với điểm $M\in OA$ thì $MB=MC$ suy ra \(\triangle MBO=\triangle MCO\Rightarrow \widehat {MBO}=\widehat{MCO}=90^0\Rightarrow MC\perp CO\)
Do đó $MC$ là tiếp tuyến của $(O)$

Ta có \(y'=-3<0\) nên hàm số luôn nghịch biến với mọi $x$ thuộc tập xác định.
Do đó kết hợp với \(x<2\) nên \(y>y(2)=-4\)
Dấu bằng không xảy ra cho nên hàm không có min.

Chọn A
Cách 1. Giả sử A (a; 0; 0) ∈ Ox, B (0;b;0) ∈ Oy, C (0;0;c) ∈ Oz.
Khi đó mặt phẳng (P) có dạng: ![]()

Do H là trực tâm tam giác ABC nên:
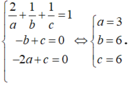
Vậy phương trình của mặt phẳng (P) là:
![]()
Cách 2. Vì tứ diện OABC có các cạnh đôi một vuông tại O và H là trực tâm tam giác ABC nên ![]() (tham khảo bài tập 4, trang 105 SGK HH11).
(tham khảo bài tập 4, trang 105 SGK HH11).
Suy ra ![]() Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
H ∈ (P) nên: 2.2 + 1 + 1 + D = 0 => D = -6
Vậy phương trình mặt phẳng là: 2x + y + z - 6 = 0


I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.