Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vật thể đi qua điểm \(A\left( {2;1} \right)\) và đi theo hướng vectơ \(\overrightarrow v \left( {3;4} \right)\).
b) Sau thời gian t thì vectơ vận tốc của vật thể là: \(t\overrightarrow v = \left( {3t;4t} \right)\).
Vậy tọa độ của vật thể sau thời gian t là: \(\overrightarrow {OA} + t\overrightarrow v = \left( {2 + 3t;1 + 4t} \right)\).

Tham khảo:
a)

Lấy điểm B(0;2) và P(0;5).
Ta có: OB=2, AB =1, MP=6 và PN=3.
Xét hai tam giác vuông OBA và MPN ta có: \(\frac{{OB}}{{MP}} = \frac{{AB}}{{PN}} = \frac{1}{3}\)
Do đó hai tam giác đồng dạng và OA // MN.
Suy ra \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng phương.
Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng hướng và MN = 3 OA.
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì \({MN} = 3. {OA} \) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.

a) Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow v = \left( {3; - 4} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {4;3} \right)\) và đi qua \(A(1;2)\)
Ta có phương trình tổng quát là
\(4(x - 1) + 3(y - 2) = 0 \Leftrightarrow 4x + 3y - 10 = 0\)
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay \(y = 0\) vào phương trình \(4x + 3y - 10 = 0\) ta tìm được \(x = \frac{5}{2}\)
Vậy \(\Delta \) cắt trục hoành tại điểm \(M\left( {\frac{5}{2};0} \right)\)


Gọi M (x; y) là vị trí của tâm bão tại thời điểm t giờ.
Tâm bão chuyển động đều từ A (13,8; 108,3) đến B (14,1;106,3).
Khi đó ta có: \(\overrightarrow {AM} = \frac{t}{{12}}.\overrightarrow {AB} \)
\(\begin{array}{l} \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(14,1 - 13,8;106,3 - 108,3)\\ \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(0,3; - 2)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{t}{{40}}\\y - 108,3 = - \frac{t}{6}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13,8 + \frac{t}{{40}}\\y = 108,3 - \frac{t}{6}\end{array} \right.\end{array}\)
Vậy tại thời điểm t giờ, tâm bão ở vị trí \(M\left( {13,8 - \frac{t}{{40}};108,3 - \frac{t}{6}} \right)\)

a) Tàu A di chuyển theo hướng vecto \(\overrightarrow {{u_1}} = \left( { - 35;25} \right)\)
Tàu B di chuyển theo hướng vecto \(\overrightarrow {{u_2}} = \left( { - 30; - 40} \right)\)
Gọi \(\alpha \) là góc giữa hai đường đi của hai tàu, ta có:
\(\cos \alpha = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {\left( { - 35} \right).\left( { - 30} \right) + 25.\left( { - 40} \right)} \right|}}{{\sqrt {{{\left( { - 35} \right)}^2} + {{25}^2}} .\sqrt {{{\left( { - 30} \right)}^2} + {{\left( { - 40} \right)}^2}} }} = \frac{1}{{5\sqrt {74} }}.\)
b) Sau t giờ, vị trí của tàu A là điểm M có tọa độ là: \(M\left( {3 - 35t; - 4 + 25t} \right)\)
Sau t giờ, vị trí của tàu B là điểm N có tọa độ là: \(N\left( {4 - 30t;3 - 40t} \right)\)
Do đó, \(\overrightarrow {MN} = \sqrt {{{\left( {1 + 5t} \right)}^2} + {{\left( {7 - 65t} \right)}^2}} = \sqrt {4250{t^2} - 900t + 50} = \sqrt {4250{{\left( {t - \frac{9}{{85}}} \right)}^2} + \frac{{40}}{{17}}} \ge \sqrt {\frac{{40}}{{17}}} \approx 1,53\left( {km} \right)\)
Suy ra MN nhỏ nhất xấp xỉ 1,53km khi \(t = \frac{9}{{85}}\)
Vậy sau \(\frac{9}{{85}}\) giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất và cách nhau 1,53km
c) Vị trí ban đầu của tàu A tại \({M_o}\) ứng với \(t = 0\) , khi đó \({M_o}\left( {3; - 4} \right)\)
Tàu B di chuyển theo đường thẳng có vecto pháp tuyến \(\overrightarrow n = \left( {40; - 30} \right)\) và đi qua điểm \(K\left( {4;3} \right)\) Phương trình tổng quát của là: \(40\left( {x - 4} \right) - 30\left( {y - 3} \right) = 0 \Leftrightarrow 4x - 3y - 7 = 0\) \(\Delta \)
Ta có: \(d\left( {{M_o},\Delta } \right) = \frac{{\left| {4.3 - 3.\left( { - 4} \right) - 7} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{17}}{5} = 3,4\left( {km} \right)\)
Vậy nếu tàu A đứng yên ở vị trí ban đầu còn tàu B di chuyển thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4km.

a)
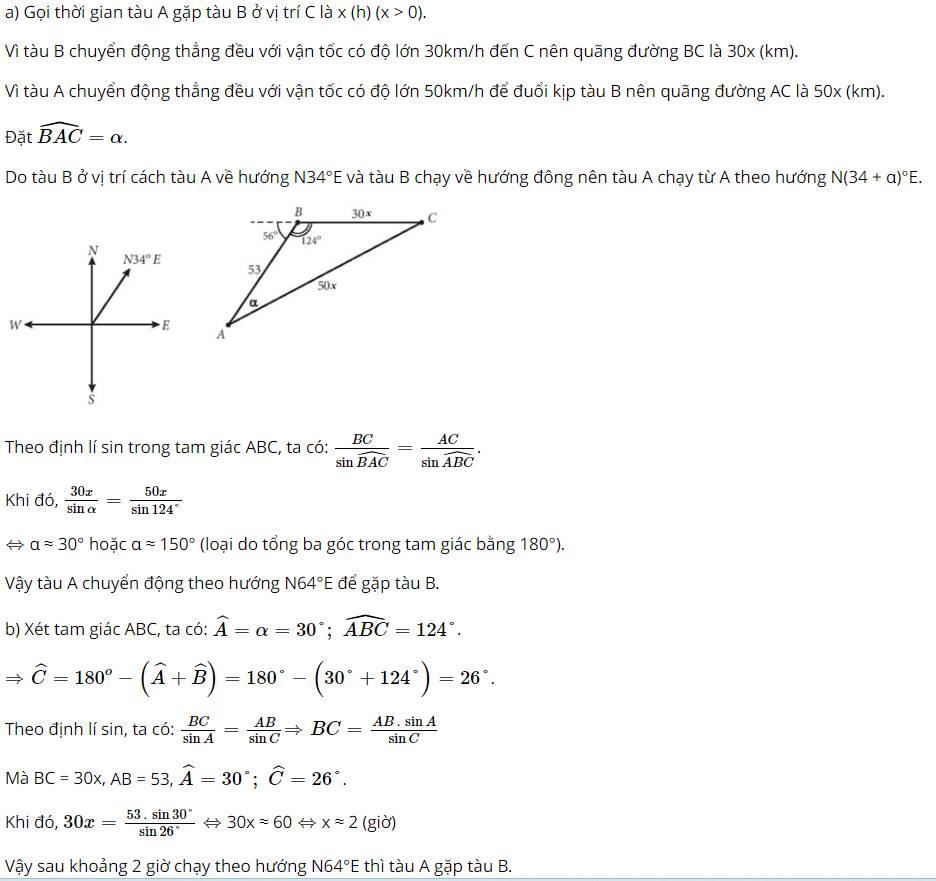
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

Khi tới vị trị M(3;4), vật bị văng khỏi quỹ đạo tròn và ngay sau đó bay theo hướng tiếp tuyến d của đường tròn tại điểm M. Do đó, d đi qua điểm M và nhận vecto \(\overrightarrow {OM} = \left( {3;4} \right)\) làm vecto pháp tuyến. Vậy phương trình của d là: \(3\left( {x - 3} \right) + 4\left( {y - 4} \right) = 0 \Leftrightarrow 3x + 4y - 25 = 0\).

Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ

a) Vị trí ban đầu ứng với \(t = 0\), suy ra vật thể ở vị trí có tọa độ là \(A\left( {2;5} \right)\).
Vị trí kết thúc ứng với \(t = 180\) , suy ra vật thể ở vị trí có tọa độ là \(B\left( {2;3} \right)\).
b) Từ đẳng thức \({\left( {\sin {t^o}} \right)^2} + {\left( {\cos {t^o}} \right)^2} = 1\) ta suy ra \({\left( {{x_M} - 2} \right)^2} + {\left( {{y_M} - 4} \right)^2} = 1\)
Do đó, M thuộc đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} = 1\)
Đường tròn có tâm \(I\left( {2;4} \right)\), bán kính \(R = 1\) và nhận AB làm đường kính.
Khi \(t \in \left[ {0;180} \right]\) thì \(\sin t \in \left[ {0;1} \right]\) và \(\cos t \in \left[ { - 1;1} \right]\). Do đó, \(2 + \sin {t^o} \in \left[ {2;3} \right]\) và \(4 + \cos {t^o} \in \left[ {3;5} \right]\).
Vậy quỹ đạo của vật thể là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm \(C\left( {3;0} \right)\) bờ AB.
Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ \(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng \(\left| {\overrightarrow v } \right|\).
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: \(\overrightarrow {AB} = 1,5.\overrightarrow v \)
\(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B(5,5; 8).