Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Trong các hàm kể trên có hàm số ở phương án A không xác định tại $x=-1$ nên hàm số đó gián đoạn tại điểm $x_0=-1$
Đáp án A.
Lời giải:
Ta chia cả tử cả mẫu cho \(x^{66}\):
\(\lim_{x\to +\infty}\frac{(x+1)(x^2+1)(x^3+1)...(x^{11}+1)}{[11x)^{11}+1]^6}=\lim_{x\to +\infty}\frac{\frac{(x+1)(x^2+1)(x^3+1)....(x^{11}+1)}{x^{66}}}{\frac{[(11x)^{11}+1]^6}{x^{66}}}\)
\(=\lim_{x\to +\infty}\frac{\left ( \frac{x+1}{x} \right )\left ( \frac{x^2+1}{x^2} \right )...\left ( \frac{x^{11}+1}{x^{11}} \right )}{\left [ \frac{(11x)^{11}+1}{x^{11}} \right ]^6}=\lim_{x\to +\infty}\frac{\left ( 1+\frac{1}{x} \right )\left ( 1+\frac{1}{x^2} \right )....\left ( 1+\frac{1}{x^{11}} \right )}{\left ( 11^{11}+\frac{1}{x^{11}} \right )^6}\)
\(=\frac{1.1...1}{(11^{11})^6}=\frac{1}{11^{66}}\)
1: Số số hạng là (2023-1):2+1=1012(số)
Tổng là S=(2023+1)*1012/2=1012^2=1024144
\(1)\) \(S=1+3+5+\cdot\cdot\cdot+2023\)
Số các số hạng của \(S\) là: \(\left(2023-1\right):2+1=1012\left(số\right)\)
Tổng \(S\) bằng: \(\left(2023+1\right)\cdot1012:2=1024144\)
\(2)\) \(S=-1+3+7+11+\cdot\cdot\cdot+1995\)
Số các số hạng của \(S\) là: \(\left[1995-\left(-1\right)\right]:4+1=500\left(số\right)\)
Tổng \(S\) bằng: \(\left[1995+\left(-1\right)\right]\cdot500:2=498500\)
#Toru
Xét cấp số cộng 1, 6, 11, ..., 96.
Ta có: 96 = 1 + 5(n − 1) ⇒ n = 20
Suy ra
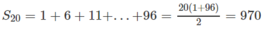
Và 2x.20 + 970 = 1010
Từ đó x = 1
Số hạng tổng quát trong khai triển \(\left(x+1\right)^n\) :\(C^k_nx^k\)
\(\Rightarrow\) hệ số của \(x^5\) trong khai triển trên:
\(\sum\limits^{12}_{n=5}C^5_n=1716\)
Chọn C
Ta có: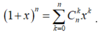 
.
Số hạng tổng quát của khai triển là: 
. Hệ số của
x
k
trong khai triển là:
C
n
k
Hệ số của số hạng chứa x 9 trong biểu thức P(x) là:
.
Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715
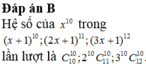
chịu. hỏi vớ vẩn