Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{3}{4}\approx\tan37^0\\ \Leftrightarrow\widehat{C}\approx37^0\)

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔBAC vuông tại A có
\(\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}=36^052'\)
=>\(\widehat{B}=53^08'\)

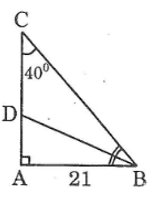
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

b: \(AH=\dfrac{AB\cdot AC}{BC}=2.4\left(cm\right)\)
HC=3,2(cm)

a) A,D,C C (O;AD)
=> DC _|_ CA
b) A,B,D C (O;AD)
=> BD _|_ AB
\(\Rightarrow\hept{\begin{cases}BD//CH\left(\perp AB\right)\\BH//CD\left(\perp AC\right)\end{cases}}\)
=> BHCD là hình bình hành
\(\Rightarrow\hept{\begin{cases}BH=DC\\BD=HC\end{cases}}\)
c) Gọi I là giao BC và AD => AI là đường trung tuyến của tam giác ABC và AHD
Mà trọng tâm của tam giác ABC và AHD đều thuộc AI và thỏa mãn \(\frac{AG}{AI}=\frac{2}{3}\)
=> 2 tam giác này cùng trọng tâm

Tham khảo tại đây nha:
https://hoc24.vn/hoi-dap/question/887221.html
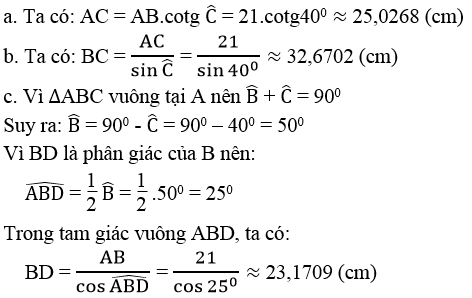
sinC=\(\dfrac{AB}{AC}\)=4/5 suy ra góc C =53 độ