Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

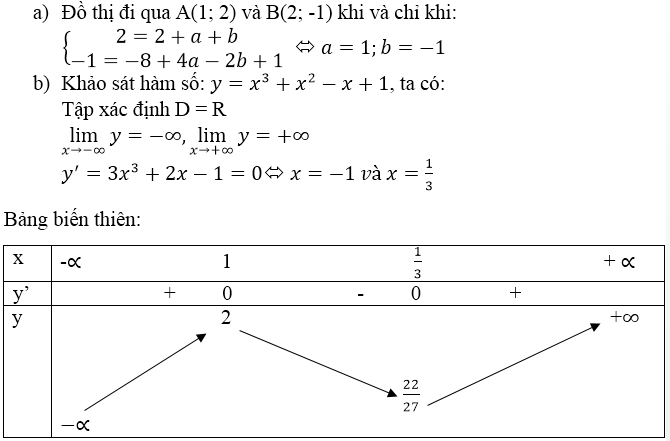
a) Học sinh tự giải
b) 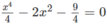
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 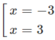
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c) 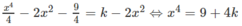
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.

a)
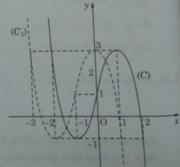
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
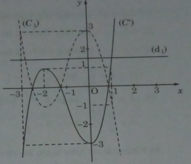
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
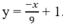
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 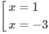
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

a) Học sinh tự làm.
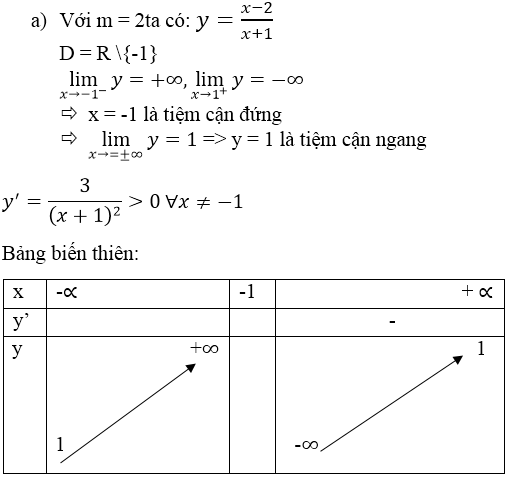
b) Tiệm cận đứng là đường thẳng x = 3.
Tiệm cận ngang là đường thẳng y = 1.
Do đó, giao điểm của hai đường tiệm cận là I(3; 1). Thực hiện phép biến đổi:
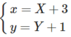
Ta được
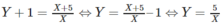
Vì Y = 5/X là hàm số lẻ nên đồ thị (C) của hàm số này có tâm đối xứng là gốc tọa độ I của hệ tọa độ IXY.
c) Giả sử M(x0; y0) ∈ (C). Gọi d1 là khoảng cách từ M đến tiệm cận đứng và d2 là khoảng cách từ M đến tiệm cận ngang, ta có:
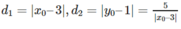
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x0 = 3 + 5 hoặc x0 = 3 - 5

Chọn D
Ta có y' = 3x2 + 6x ⇒ k = y'(1) = 9.
Phương trình tiếp tuyến tại M(1;4) là
d: y = y'(x0)(x - x0) + y0 = 9(x - 1) + 4 = 9x - 5.

b) Ta có \(y'=4x^3-4x;y\left(-2\right)=8;y'\left(-2\right)=-24\)
Phương trình tiếp tuyến phải tìm là :
\(y-y\left(-2\right)=y'\left(-1\right)\left(x+2\right)\)
\(\Leftrightarrow y-8=-24\left(x+2\right)\Leftrightarrow y=-24x-10\)

a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10
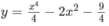
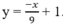
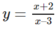
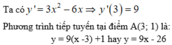
a) TXĐ: R
📷
y’>0 trên khoảng (-∞; -2)và (0; +∞)
y'<0 trên khoảng (-2; 0)
yCĐ=y(-2)=0; yCT=y(0)=-4
📷
y”=6x+6=6(x+1)=0 <=> x = -1
Bảng xét dấu y’’
X-∞-1+∞Y’’–0+Đồ thịLồiđiểm uốn u(-1; -2)lõm
Hàm số lồi trên khoảng (-∞; -1)
Hàm số lõm trên khoảng -1; +∞)
Hàm số có 1 điểm uốn u(-1; -2)
Bảng biến thiên:
📷
Đồ thị
Đi qua điểm (1; 0) và (-3; -4)
b) Hàm số y=x3+3x2-4 có điểm uốn u(-1; -2)
Ta có: y’=3x2-4 ; y’(-1) = -3
Phương trình tiếp tuyến tại điểm uốn u(-1; -2) có dạng
y-y0=y'(x0)(x-x0)
<=> y+2=-3(x+1)
<=> y=-3x-5
Vậy phương trình tiếp tuyến tại điểm uốn là: y = -3x – 5.
📷
c) Đồ thị nhận I(-1; -2) là tâm đối xứng khi và chỉ khi:
f(x0+x)+f(x0-x)=2y0 với ∀x
<=> f(x-1)+f(-x-1)=-4 ∀x
<=> (x-1)3+3(x-1)2-4+(-1-x)3+3(-1-x)2-4 ∀x
<=> x3-3x2+3x-1+3x2-6x+3-5-3x-3x2-x3+3+6x+3x2-4=-4 ∀x
<=>-4=4 ∀x
=> I(-1; -2) là tâm đối xứng của đồ thị.
bạn vào chính câu hỏi này của bạn trong bingbe xem