ĐỀ SỐ 1
Thời gian làm bài: 120 phút
Câu 1: (2 điểm) Cho biểu thức:

a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số  sao cho
sao cho 
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n thuộc N*. Hãy so sánh 
b. Cho  . So sánh A và B.
. So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ: a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.
ĐỀ SỐ 2
Thời gian làm bài: 120 phút
Câu 1:
a. Tìm các số tự nhiên x, y. sao cho (2x + 1)(y – 5) = 12
b.Tìm số tự nhiên sao cho 4n-5 chia hết cho 2n-1
c. Tìm tất cả các số  , biết rằng số B chia hết cho 99
, biết rằng số B chia hết cho 99
Câu 2.
a. Chứng tỏ rằng  là phân số tối giản.
là phân số tối giản.
b. Chứng minh rằng: 
Câu 3:
Một bác nông dân mang cam đi bán. Lần thứ nhất bán 1/2số cam và 1/2 quả; Lần thứ 2 bán 1/3 số cam còn lạivà 1/3 quả; Lần thứ 3 bán 1/4 số cam còn lại và 3/4 quả. Cuối cùng còn lại 24 quả. Hỏi số cam bác nông dân đã mang đi bán.
Câu 4:
Cho 101 đường thẳng trong đó bất cứ hai đường thẳng nào cũng cắt nhau, không có ba đường thẳng nào đồng quy. Tính số giao điểm của chúng.
ĐỀ SỐ 3
Thời gian làm bài: 120 phút
Bài 1: (1,5 điểm) Tìm x
a) 5x = 125; b) 32x = 81;
c) 52x-3 – 2.52 = 52.3;
Bài 2: (1,5 điểm)
Cho a là số nguyên. Chứng minh rằng: |a| < 5 ↔ - 5 < a < 5
Bài 3: (1,5 điểm)
Cho a là một số nguyên. Chứng minh rằng:
a. Nếu a dương thì số liền sau a cũng dương.
b. Nếu a âm thì số liền trước a cũng âm.
c. Có thể kết luận gì về số liền trước của một số dương và số liền sau của một số âm?
Bài 4: (2 điểm)
Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng tổng của 31 số đó là số dương.
Bài 5: (2 điểm)
Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tuỳ ý sau đó đem cộng mỗi số với số chỉ thứ tự của nó ta được một tổng. Chứng minh rằng trong các tổng nhận được, bao giờ cũng tìm ra hai tổng mà hiệu của chúng là một số chia hết cho 10.
Bài 6: (1,5 điểm)
Cho tia Ox. Trên hai nữa mặt phẳng đối nhau có bờ là Ox. Vẽ hai tia Oy và Oz sao cho góc xOy và xOz bằng 1200. Chứng minh rằng:
a. Góc xOy = xOz = yOz
b. Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại





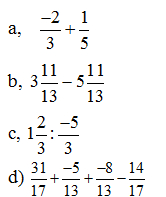
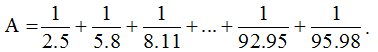

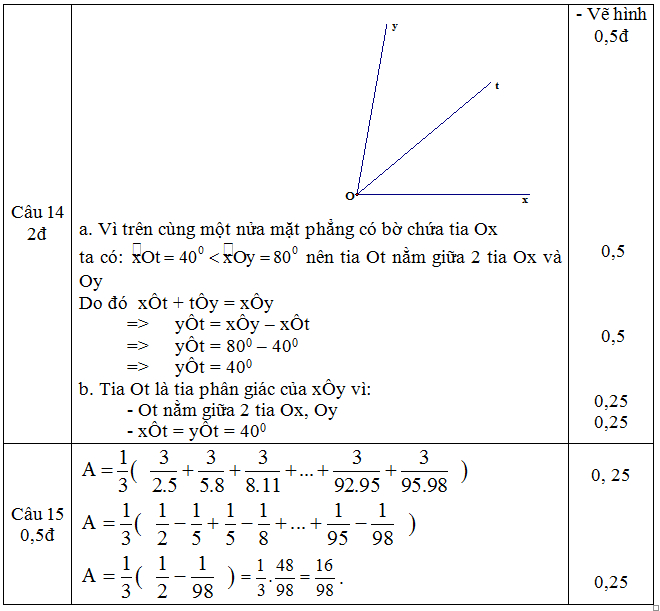
Bài 5:
a) Ta có: \(\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)
\(\Rightarrow\widehat{zOx}=\widehat{xOy}-\widehat{yOz}=180^0-80^0=100^0\)
b) Hai góc có phụ nhau vì:
OM là tia phân giác \(\widehat{xOz}\Rightarrow\widehat{mOz}=\frac{1}{2}\widehat{xOz}\)
ON là tia phân giác \(\widehat{yOz}\Rightarrow\widehat{nOz}=\frac{1}{2}\widehat{yOz}\)
=> \(\widehat{mOz}+\widehat{nOz}=\widehat{mOn}=\frac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=\frac{1}{2}\widehat{xOy}=\frac{1}{2}180^0=90^0\)
Bài 4:
a) Số học sinh giỏi của lớp là:
\(40\cdot\frac{1}{5}=8\left(em\right)\)
Số học sinh trung bình của lớp là:
\(\left(40-8\right)\cdot\frac{3}{8}=12\left(em\right)\)
Số học sinh khá của lớp là:
40-8-12=20 (em)
b) Tỉ số phần trăm của học sinh trung bình đối với cả lớp là:
12:40 x 100=30%
Bài 5:
x O y z n m
a) Có \(\widehat{xOy}\)là góc bẹt => \(\widehat{xOy}=180^o\)
Vì tia từ O vẽ tia Oz sao cho góc yOz=80\(^o\)
=> \(\widehat{xOz}=\widehat{xOy}-\widehat{yOz}\)
Thay \(\widehat{xOy}=180^o\left(cmt\right);\widehat{yOz}=80^o\left(gt\right)\)
=> \(\widehat{xOz}=180^0-80^o=100^o\)
Vậy góc xOz=100\(^o\)
b) Vì Om và On lần lượt là phân giác của góc xOz và góc yOz (gt)
\(\Rightarrow\hept{\begin{cases}\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}=\frac{100^0}{2}=50^o\\\widehat{zOn}=\widehat{nOy}=\frac{\widehat{zOy}}{2}=\frac{80^o}{2}=40^o\end{cases}}\)
\(\Rightarrow\widehat{mOz}+\widehat{zOn}=50^o+40^o=90^o\)
=> Góc mOz và zOn có phụ nhau