
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

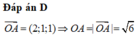

Đáp án A
Phương trình mặt phẳng (ABC) là x 1 + y 3 + z 2 = 1 mà D 1 ; 3 ; - 2 ⇒ D ∈ A B C .
Và ta thấy rằng A C ¯ = - 1 ; 0 ; 2 và B D ¯ = - 1 ; 0 ; 2 suy ra ABCD là hình bình hành.
Vậy O.ABCD là một hình chóp có đáy là hình bình hành, do đó có 5 mặt phẳng thỏa mãn yêu cầu gồm:
Mặt phẳng đi qua trung điểm của AC,BD và song song với (SAD) hoặc (SBC).
Mặt phẳng đi qua trung điểm cuả AD,BC đồng thời song song với (SAC) hoặc (SBD).
Mặt phẳng đi qua trungđiểm của OA,OB,OC,OD.

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
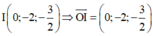
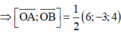
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B

Chọn C.
Phương pháp: Dùng công thức tính khoảng cách từ điểm đến đường thẳng.
Cách giải:
