Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Viết lại 
Suy ra (S) có tâm I(a;b;c), 
Nhận thấy 
tiếp xúc với mặt phẳng (Oxy).
Chọn B.
Phương trình mặt chắn của mặt phẳng (ABC) là: 
Từ giả thiết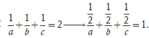 
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Đáp án A
Phương pháp:
+) Viết phương trình mặt phẳng (ABC) ở dạng đoạn chắn, thay tọa độ điểm M vào pt mặt phẳng (ABC).
+) (ABC) tiếp xúc với mặt cầu (S) tâm I bán kính R ó d(I;(ABC)) = R
Cách giải:
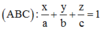
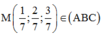
(ABC) tiếp xúc với mặt cầu (S) có tâm I(1;2;3) và bán kính R = 72 7
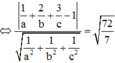
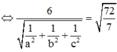
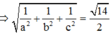
Chọn B.
Phương pháp : Số đo góc tạo bởi hai mặt phẳng hoặc bằng góc giữa hai véc tơ pháp tuyến hoặc bù với hai véc tơ pháp tuyến và góc giữa hai mặt phẳng là góc không tù.
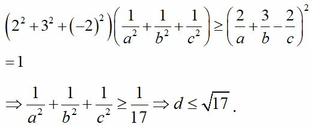
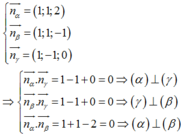
Đáp án D.
Gọi O là trung điểm của AB, suy ra O 0 ; 0 ; 0 .
Ta có A B → = − 2 x 0 ; 0 ; 0 , O C → = 0 ; 1 ; 0 ⇒ A B → . O C → = 0 ⇒ A B ⊥ O C .
Gắn hệ trục tọa độ Oxyz như hình vẽ bên. Với A x 0 ; 0 ; 0 , B − x 0 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − x 0 ; 0 ; 4 − x 0 , A ' x 0 ; 0 ; 4 − x 0 , C ' 0 ; 1 ; 4 − x 0 do x 0 + y 0 = 4 và 0 < x 0 , y 0 < 4 .
Có A C ' → = − x 0 ; 1 ; 4 − x 0 , B ' C → = x 0 ; 1 ; x 0 − 4 ⇒ A C ' → , B ' C → = 2 x 0 − 8 ; 0 ; − 2 x 0
A C → = − x 0 ; 1 ; 0 ⇒ A C ' → , B ' C → . A C → = − x 0 2 x 0 − 8 = − 2 x 0 x 0 − 4
⇒ d A C ' ; B ' C = A C ' → , B ' C → . A C → A C ' → , B ' C → = 2 x 0 x 0 − 4 4 4 − x 0 2 + 4 x 0 2 = x 0 4 − x 0 4 − x 0 2 + x 0 2
do x 0 ∈ 0 ; 4 .
Với 0 < x 0 < 4 , ta có 4 − x 0 2 + x 0 2 ≥ A M − G M 2 4 − x 0 2 x 0 2 = 2 x 0 4 − x 0 .
Như vậy d A C ' ; B ' C = x 0 4 − x 0 4 − x 0 2 + x 0 2 ≤ x 0 4 − x 0 2 x 0 4 − x 0 = 1 2 .
Dấu “=” xảy ra khi x 0 = 4 − x 0 ⇔ x 0 = 2 = y 0 .
Khi đó A 2 ; 0 ; 0 , B − 2 ; 0 ; 0 , C 0 ; 1 ; 0 , B ' − 2 ; 0 ; 2 . Giả sử phương trình mặt cầu ngoại tiếp lăng trụ A B C . A ' B ' C ' là .
Ta có hệ phương trình sau:
2 2 + 0 2 + 0 2 − 2 a .2 − 2 b .0 − 2 c .0 + d = 0 − 2 2 + 0 2 + 0 2 − 2 a − 2 − 2 b .0 − 2 c .0 + d = 0 0 2 + 1 2 + 0 2 − 2 a .0 − 2 b .1 − 2 c .0 + d = 0 − 2 2 + 0 2 + 2 2 − 2 a − 2 − 2 b .0 − 2 c .2 + d = 0 ⇔ 4 a − d = 4 4 a + d = − 4 2 b − d = 1 4 a − 4 c + d = − 8 ⇔ a = 0 b = − 3 2 c = 1 d = − 4
Vậy mặt cầu (S) có tâm I 0 ; − 3 2 ; 1 và bán kính
R = a 2 + b 2 + c 2 − d = 29 2