Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Trong không gian, với tam giác đều bất kì ABC có bốn mặt phẳng đối xứng.
Đó là: Ba mặt phẳng trung trực của ba cạnh và mặt phẳng chứa .

Đường thẳng d có vectơ chỉ phương \(\overrightarrow{u}\left(-2;2;1\right)\) và đi qua \(M\left(3;6;1\right)\)
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow{AB}\left(-4;-2;5\right)\) và đi qua \(\overrightarrow{AM}\left(-1;4;-1\right)\)
Ta có \(\left[\overrightarrow{u},\overrightarrow{AB}\right]=\left(12;6;12\right)\Rightarrow\left[\overrightarrow{u},\overrightarrow{AB}\right].\overrightarrow{AM}=-12+24-12=0\)
Vậy ta có AB và d đồng phẳng.
\(C\in d\Rightarrow C\left(3-2t;6+2t;1+t\right)\)
Tam giác ABC cân tại A \(\Leftrightarrow AB=AC\)
\(\Leftrightarrow\left(1+2t\right)^2+\left(4+2t\right)^2+\left(1-t\right)^2=45\)
\(\Leftrightarrow9t^2-18t-27=0\)
\(\Leftrightarrow t=1\) hoặc \(t=-3\)
Vậy \(C\left(1;8;2\right)\) hoặc \(C\left(9;0;-2\right)\)
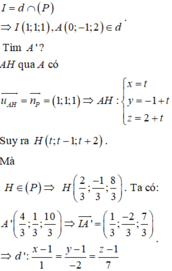



Chọn D.
Trong không gian, với tam giác đều bất kì ABC có bốn mặt phẳng đối xứng.
Đó là: Ba mặt phẳng trung trực của ba cạnh và mặt phẳng chứa ΔABC.