Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

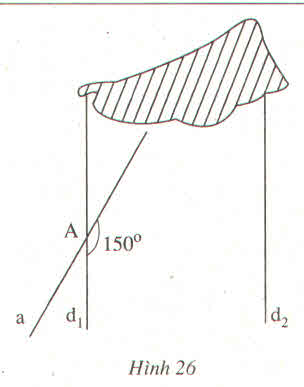
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.

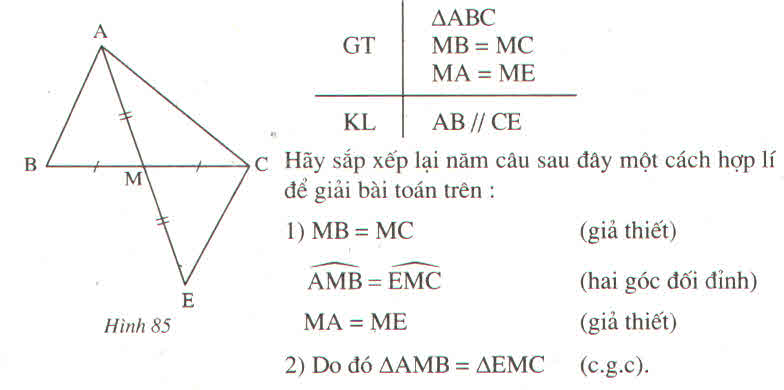
Cho tam giác abc vuông cân ở a ,m là trung điểm của bc, điểm e nằm giữa m và c.Ke bh,ck vuông với ae (h,k€ae) chứng minh bh=ak.C/m tam giác mbh= tam giác mak.C/m tam giác mhklaf tam giác vuông cân .Vex hình luôn cho mình mình cần gấpkhoang 6 tiênd nữa

a, Xét △OAC vuông tại A và △OBD vuông tại B
Có: OA = OB (gt)
COA = DOB (2 góc đối đỉnh)
=> △OAC = △OBD (cgv-gnk)
b, Xét △OCE và △ODE cùng vuông tại O
Có: OE là cạnh chung
OC = OD (△OAC = △OBD)
=> △OCE = △ODE (2cgv)
c, Ta có: DE = BE + BD mà BD = AC (△OBD = △OAC) ; CE = DE (△OCE = △ODE)
=> CE = BE + AC (đpcm)
ý AC = 1/2 BC còn có điều kiện gì nữa ko??
Tìm cách giải
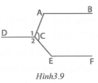
Trong hình vẽ đã có các cặp góc so le trong là A ^ và C 1 ^ ; E ^ và C 2 ^ . Muốn chứng tỏ AB // CD và CD // EF chỉ cần chứng tỏ A ^ = C 1 ^ và E ^ = C 2 ^ .
Trình bày lời giải
Ta có A C E ^ = C 1 ^ + C 2 ^ 2 ⇒ C 1 ^ + C 2 ^ = 2 A C E ^ .
Mặt khác C 1 ^ + C 2 ^ + A C E ^ = 360 ° nên 2 A C E ^ + A C E ^ = 360 ° ⇒ A C E ^ = 120 ° .
Do đó C 1 ^ + C 2 ^ = 360 ° − 120 ° = 240 ° mà C 1 ^ − C 2 ^ = 20 ° nên C 1 ^ = 130 ° ; C 2 ^ = 110 ° .
Ta có A C E ^ = A ^ + E ^ 2 ⇒ A ^ + E ^ = 2 A C E ^ = 240 ° .
Lại có A ^ − E ^ = 20 ° nên A ^ = 130 ° ; E ^ = 110 ° .
Ta có A ^ = C 1 ^ = 130 ° ⇒ A B / / C D ; E ^ = C 2 ^ = 110 ° ⇒ C D / / E F vì có cặp góc so le trong bằng nhau.
Vận dụng cặp góc đồng vị