Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này trong SGK lớp 7 đơn giản mà bạn
Giải
Theo đề bài: \(x=\frac{a}{m}\),\(y=\frac{b}{m}\)\(\left(a,b,m\in Z,\ne0\right)\)
Vì \(x< y\) nên \(a< b\)
Ta có: \(x=\frac{2a}{2m}\),\(y=\frac{2b}{2m}\),\(z=\frac{a+b}{2m}\)
a < b nên a + a < a + b hay \(2a< a+b\) ( 1 )
a < b nên a + b < b + b hay \(a+b< 2b\) ( 2 )
Từ ( 1 ) và ( 2 ) ta có 2a < a + b < 2b.
\(\Rightarrow\) \(\frac{2a}{2m}< \frac{a+b}{2m}< \frac{2b}{2m}\)hay \(x< y< z\)
♥♥♥ Ủng hộ cho mk nha ♥♥♥
Vì x<y
=> \(\frac{a}{m}< \frac{b}{m}\)
=> a<b
x= \(\frac{a}{m};z=\frac{a+b}{2m}\)
=> x=\(\frac{2a}{2m}< \frac{a+b}{2m}\)=z
=> 2a<a+b
=> x<z
mặt khác z<y nên
=> z=\(\frac{a+b}{2m}< \frac{b}{m}\)=y
=>\(\frac{a+b}{2m}< \frac{2b}{2m}\)
=> a+b< 2b
=> z<y
=> x<z<y hay \(\frac{a}{m}< \frac{b}{m}< \frac{a+b}{2m}\)

Ta có: \(\frac{a+1}{b+1}-\frac{a}{b}=\frac{b\left(a+1\right)}{b\left(b+1\right)}-\frac{a\left(b+1\right)}{b\left(b+1\right)}=\frac{ab+b-ab-a}{b\left(b+1\right)}=\frac{b-a}{b\left(b+1\right)}=\frac{1}{b\left(b+1\right)}\left(b-a\right)\)
Vì a < b => (b - a) > 0
\(\Rightarrow\frac{1}{b\left(b+1\right)}\left(b-a\right)>0\)\(\Rightarrow\frac{a+1}{b+1}-\frac{a}{b}>0\)\(\Rightarrow\frac{a+1}{b+1}>\frac{a}{b}\)

Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
Theo đề bài ta có x = \(\frac{a}{m}\), y = \(\frac{b}{m}\)(a, b, m ∈ Z, b # 0)
Vì x < y nên ta a < b
Ta có: x = \(\frac{2a}{2m}\), y = \(\frac{2b}{2m}\); z = \(\frac{a+b}{2m}\)
Vì a < b \(\Rightarrow\) a + a < a + b \(\Rightarrow\) 2a < a + b
Vì 2a < a + b nên x < z (1)
Vì a < b \(\Rightarrow\) a + b < b + b \(\Rightarrow\) a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta \(\Rightarrow\) x < z < y

Hoàng Anh Thư mk nghĩ x = \(\frac{a}{m}\) , như tkế mk làm đc , còn như x = \(\frac{a}{b}\) tkì mk chịu thôi !!
![]()

a, Ta có: \(\dfrac{a}{a+b+c}< \dfrac{a}{a+b}< \dfrac{a+c}{a+b+c}\) (1)
\(\dfrac{b}{a+b+c}< \dfrac{b}{b+c}< \dfrac{b+a}{a+b+c}\) (1)
\(\dfrac{c}{a+b+c}< \dfrac{c}{c+a}< \dfrac{c+b}{a+b+c}\) (3)
Từ (1), (2), (3) \(\Rightarrow\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}< \dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< \dfrac{a+c}{a+b+c}+\dfrac{b+a}{a+b+c}+\dfrac{c+b}{a+b+c}\Rightarrow1< \dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< 2\)
Thầy mk hướng dẫn phần a như thế còn phần b mk ko bt lm, chúc p hk tốt ![]()

Ta có: \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\left(b>0,d>0\right)\)
a) Giả sử: +) \(\dfrac{a}{b}=\dfrac{c}{d}\) \(\Rightarrow\) \(ad=bc\) (nhân chéo)
\(\Rightarrow\) nếu \(\dfrac{a}{b}< \dfrac{c}{d}\) thì \(ad< bc.\)
b) Giả sử \(ad=bc\) \(\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\) nếu \(ad< bc\) thì \(\dfrac{a}{b}< \dfrac{c}{d}.\)


Để \(\dfrac{a}{b}< \dfrac{a+c}{b+d}\) thì a(b+d) < b(a+c)
<=> ab + ad < ba + cb
<=> ad < cb
<=> \(\dfrac{a}{b}< \dfrac{c}{d}\)
Để \(\dfrac{a+c}{b+d}< \dfrac{c}{d}\) thì (a+c)d < (b+d)c
<=> ad + cd < bc + dc
<=> ad < bc
<=> \(\dfrac{a}{b}< \dfrac{c}{d}\)
Chúc bạn học tốt!
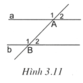
Ta có A 1 ^ + A 2 ^ + B 2 ^ = a ° ⇒ B 2 ^ = a ° − 180 ° (1)
B 1 ^ + B 2 ^ + A 1 ^ = b ° ⇒ A 1 ^ = b ° − 180 ° (2)
Từ (1) và (2), suy ra: B 2 ^ + A 1 ^ = a ° + b ° − 360 ° = 540 ° − 360 ° = 180 ° .
Mặt khác A 2 ^ + A 1 ^ = 180 ° (kề bù) nên B 2 ^ + A 1 ^ = A 2 ^ + A 1 ^ = 180 ° .
Suy ra B 2 ^ = A 2 ^ . Do đó a // b vì có cặp góc đồng vị bằng nhau