Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

15p = 1/4h; 30p = 1/2h
đi ngược chiều: (v1 + v2).1/4 = 20 (1)
đi cùng chiều: v1.1/2 -20 = v2.1/2 (2)
từ (1) và (2) có : \(\begin{cases}v_1+v_2=80\\v_1-v_2=40\end{cases}\)
đến đây trở thành bài toán: tổng-tỷ lop4 đã học giải ra:
v1 = 60km/h
v2 =20 km/h
ở đâu ra 1 ng vi diệu đến z, ta nói: 1 bài lop10 mà làm theo kiến thức lop7 nó nhẹ nhàng, dễ hiu quá đi thôi

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

B. Sau thời gian 2,5s thì vật dừng lại, sau đó tiếp tục chuyển động nhanh dần đều. Vận tốc của nó lúc t=5s là v = -10m/s

a) chất điểm chuyển động thẳng nhanh dần đều
(vì khi so sánh ta có : \(x=x_0+v_0t+\dfrac{1}{2}at^2\) với \(x=-100+t^2\) ta tìm được \(a=2\) ; \(x_0=-100\) và \(v_0=0\))
và theo chiều dương vì nếu cứ tính tọa bằng công thức \(x=-100+t^2\)
thì tọa độ \(x\) có xu hướng đi về phái chiều dương .
b) ta có : \(v=v_0+at=0+2.10=20\left(m\backslash s\right)\)
c) ta có quảng đường mà chất điểm đi trong 20s đầu
là : \(S=v_0t+\dfrac{1}{2}at^2=0.20+\dfrac{1}{2}.2.20^2=400\)
và quảng đường mà chất điểm đi trong 10s đầu
là : \(S=v_0t+\dfrac{1}{2}at^2=0.10+\dfrac{1}{2}.2.10^2=100\)
\(\Rightarrow\) quảng đường chất điểm đi được từ \(t=10s\) đến \(t=20s\)
là : \(400-100=300m\)
vậy quảng đường vật đi được từ \(t=10s\) đến \(t=20s\) là \(300m\)

Gọi \(t\left(s\right)\)là thời gian để hai xe đuổi kịp nhau. \(\left(t>0\right)\)
Ta có: \(4t+\frac{1}{2}.0,2t^2=200+1.t+\frac{1}{2}.0,1.t^2\)
\(\Leftrightarrow\frac{1}{20}t^2+3t-200=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=40\left(tm\right)\\t=-100\left(l\right)\end{cases}}\)
Vị trí hai xe gặp nhau cách A quãng đường là: \(4.40+\frac{1}{2}.0,2.40^2=320\left(m\right)\)

a) \(x=4+2t^2=4+\frac{1}{2}.4t^2\)
So sánh với phương trình của chuyển động biến đổi đều \(x=x_0+v_0t+\frac{1}{2}at^2\) ta thấy
\(v_0=0;a=4\)m/s2.
b) Thay t = 5s vào ta được quãng đường đi được là
\(s=\left|x-x_0\right|=\left|2.t^2\right|=2.5.5=50m.\)
c) \(v=v_0+at=4t\) Thay v = 45 m/s \(\Rightarrow t=\frac{45}{4}=11,25s.\)
Quãng đường đi được là
\(s'=\left|2t^2\right|=2.11,25^2=253,125m.\)
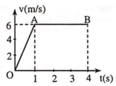
 tham khảo nếu sai thì thôi :v
tham khảo nếu sai thì thôi :v
a) Gia tốc trên đoạn OA: a 1 = Δ v Δ t = 6 1 = 6 m/s2.
Trên đoạn AB chất điểm chuyển động thẳng đều nên gia tốc a 2 = 0 .
b) Quãng đường chất điểm đi trong 1s đầu tiên: s 1 = 1 2 a 1 t 1 2 = 1 2 .6.1 2 = 3 m.
Quãng đường chất điểm đi trong 2s kế tiếp: s 2 = v t 2 = 6.2 = 12 m.
Quãng đường chất điểm đi trong 3s đầu tiên: s 2 = v t 2 = 6.2 = 12 m.
c) Thời điểm mà chất điểm có vận tốc 2,4m/s: t = v a = 2 , 4 6 = 0 , 4 s.