
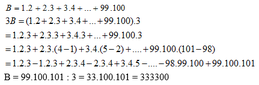
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

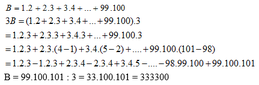

Ta có: \(S=1.2+2.3+3.4+...+99.100\)
\(\Rightarrow3S=1.2.3+2.3.3+3.3.4+....+99.100.3\)
\(\Rightarrow3S=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)....99.100.\left(101-98\right)\)
\(\Rightarrow3S=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+99.100.101-98.99.100\)
\(\Rightarrow3S=99.100.101\)
\(\Rightarrow S=\frac{99.100.101}{3}=\frac{999900}{3}=333300\)

đặt A=1.2+2.3+...+99.100
=>3A=1.2.3+2.3.3+...+99.100.3
=1.2.3+2.3.(4-1)+...+99.100(101-98)
=1.2.3+2.3.4-1.2.3+...+99.100.101-98.99.100
=99.100.101=999900
=>A=999900:3=333300



\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=\frac{1}{1}-\frac{1}{100}\)
\(=\frac{99}{100}\)


\(\frac{2}{1.2}+\frac{2}{2.3}+\frac{2}{3.4}+......+\frac{2}{99.100}\)
\(=2.\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.....+\frac{1}{99.100}\right)\)
\(=2.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+......+\frac{1}{99}-\frac{1}{100}\right)\)
\(=2.\left(1-\frac{1}{100}\right)\)
\(=2.\frac{99}{100}=\frac{99}{50}\)
=\(2\left(\frac{1}{1.2}+\frac{1}{2.3}+..+\frac{1}{99.100}\right)\)
=\(2\left(1-\frac{1}{100}\right)\)
=\(2\cdot\frac{99}{100}=\frac{99}{50}\)

\(B=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\)
\(B=\frac{1}{1}-\frac{1}{100}\)
\(B=\frac{99}{100}\)
\(B=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.....+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
\(=\frac{99}{100}\)


Ta có :
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{98.99}+\frac{1}{99.100}\)
\(=\)\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{98}-\frac{1}{99}+\frac{1}{99}-\frac{1}{100}\)
\(=\)\(1-\frac{1}{100}\)
\(=\)\(\frac{99}{100}\)
Vậy \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{98.99}+\frac{1}{99.100}=\frac{99}{100}\)
Chúc bạn học tốt ~
\(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+...+\frac{1}{99\cdot100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}=\frac{99}{100}\)
ĐÚNG 100%