Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

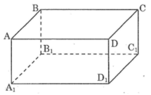
a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.

Ta có AD vuông góc với D1D vì A1D1DA là hình chữ nhật
Tương tự => DC cũng vuông góc với D1D
Mà AD chỉ vuông góc với DC vì ABCD là hình chữ nhật mà thôi chứ không song song
=> Mệnh đề trên là sai
(>Tích đúng cho mình nha<) ![]()

Ta có: mp(ABCD) // mp(A1B1C1D1)
AB thuộc mp(ABCD)
A1D1 thuộc mp(A1B1C1D1)
AB không song song với A1D1
Vậy mệnh đề đã cho sai.

Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou

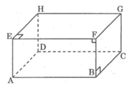
Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a) sai.

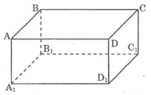
Ta có:AB ⊥ BC
C C 1 ⊥ BC
Nhưng AB và C C 1 không song song với nhau
Vậy mệnh đề đã cho là sai
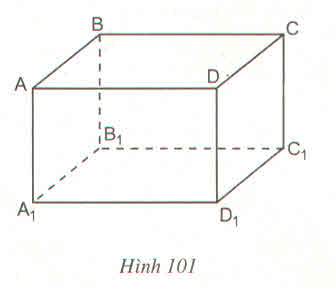



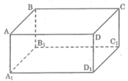
Vậy mệnh để b) sai.