Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để hàm số đồng biến trên R thì:
\(y'=(m+2)x^2+2mx+1\geq 0\forall x\in\mathbb{R}\)
Theo định lý về dấu của tam thức bậc 2 thì điều này xảy ra khi :
\(\left\{\begin{matrix} m+2> 0\\ \Delta'=m^2-m-2\leq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m> -2\\ (m+1)(m-2)\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m> -2\\ -1\leq m\leq 2\end{matrix}\right.\)
\(\Leftrightarrow -1\leq m\leq 2\)
Đáp án B

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

Ta có : \(y'=-x^2+2mx+m-2\Rightarrow\Delta'=m^2+m-2\)
Hàm số đồng biến trên đoạn có độ dài bằng 4 <=> phương trình y' =0 có 2 nghiệm phân biệt \(x_1;x_2\) và thỏa mãn :
\(\left|x_1-x_2\right|=4\Leftrightarrow\begin{cases}\Delta'>0\\\left|x_1-x_2\right|=4\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\\left(x_1+x_2\right)^2-4x_1.x_2=16\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\4m^2+4\left(m-2\right)=16\end{cases}\)
\(\Leftrightarrow m=2\) hoặc \(m=-3\)
Kết luận \(m=2\) hoặc \(m=-3\) thì hàm số đồng biến trên đoạn có độ dài bằng 4

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

3.
- Với \(m=1\Rightarrow f\left(x\right)=-9x\) nghịch biến trên R (ko thỏa mãn)
- Với \(m=-1\Rightarrow f\left(x\right)=9x\) đồng biến trên R (thỏa mãn)
- Với \(m\ne\pm1\)
\(f'\left(x\right)=6\left(m^2-1\right)x^2-9m\ge0;\forall x>1\)
TH1: \(\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)\le0\end{matrix}\right.\) \(\Rightarrow m< -1\)
TH2: \(\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)>0\\x_1< x_2\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)>0\\\sqrt{\frac{3m}{2\left(m^2-1\right)}}\le1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\3m\le2m^2-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\2m^2-3m-2\ge0\end{matrix}\right.\)
\(\Rightarrow m\ge2\)
Vậy \(\left[{}\begin{matrix}m\le-1\\m\ge2\end{matrix}\right.\)
2.
\(\Leftrightarrow y'=2m-\frac{x+1}{\sqrt{x^2+2x+11}}\ge0;\forall x\in R\)
\(\Leftrightarrow2m\ge\frac{x+1}{\sqrt{x^2+2x+11}}\)
\(\Leftrightarrow m\ge\frac{x+1}{2\sqrt{x^2+2x+11}}\)
\(\Leftrightarrow m\ge\max\limits_Rf\left(x\right)\) với \(f\left(x\right)=\frac{x+1}{2\sqrt{x^2+2x+11}}\)
Ta có: \(f'\left(x\right)=\frac{5}{\sqrt{\left(x^2+2x+11\right)^3}}>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\frac{x+1}{2\sqrt{x^2+2x+11}}=\frac{1}{2}\)
\(\Rightarrow f\left(x\right)< \frac{1}{2};\forall x\in R\)
\(\Rightarrow m\ge\frac{1}{2}\)

Ta có \(y'=-\left(m-1\right)x^2+2\left(m+2\right)+3m\) \(\Rightarrow\) Hàm đồng biến trên khoảng \(\left(-\infty;-2\right)\Leftrightarrow y'\ge0,x\in\left(-\infty;-2\right)\)(*)
Vì y'(x) liên tục tại x = -2 nên (*) \(\Leftrightarrow y'\ge0;\)
và mọi x thuộc (-\(-\infty;2\) ] (*)
\(\Leftrightarrow-\left(m-1\right)x^2+2\left(m+2\right)x+3m\ge0\), mọi x thuộc (-\(-\infty;2\) ]
\(\Leftrightarrow m\left(-x^2+2x+3\right)\ge-x^2-4x\), mọi x thuộc (-\(-\infty;2\) ]\(\Leftrightarrow m\le g\left(x\right)\), mọi x thuộc (-\(-\infty;2\) ] (Trong đó \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\))
\(\Leftrightarrow m\le Min_{\left(-\infty;-2\right)}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\) trên đoạn (-\(-\infty;2\) ]
\(\Rightarrow g'\left(x\right)=\frac{-6\left(x^2+x+2\right)}{\left(-x^2+2x+3\right)^2}=\frac{-6\left(x+\frac{1}{2}\right)^2+\frac{7}{4}}{\left(-x^2+2x+3\right)^2}<0\),mọi x thuộc (-\(-\infty;2\) ]
\(\Rightarrow g\left(x\right)\) là hàm số nghịch biến trên (-\(-\infty;2\) ]
\(\Rightarrow Min_{\left(-\infty;-2\right)}g\left(x\right)=g\left(-2\right)=-\frac{4}{5}\)
Vậy \(m\le-\frac{4}{5}\) thì hàm số đồng biến trên khoảng \(\left(-\infty;-2\right)\)

Ta có : \(y'=4x^3-4\left(m-1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m-1\right)x=0\Leftrightarrow x\left[x^2-\left(m-1\right)\right]=0\)
Trường hợp 1 : nếu \(m-1\le0\Leftrightarrow m\le1\), hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\), vậy \(m\le1\) thỏa mãn yêu cầu bài toán
Trường hợp 2 : nếu \(m-1>0\Leftrightarrow m>1\), hàm số đồng biến trên khoảng \(\left(-\sqrt{m-1};0\right)\) và \(\left(\sqrt{m-1};+\infty\right)\)
Để hàm số đồng biến trên khoảng (1;3) thì \(\left(\sqrt{m-1}\le1\Leftrightarrow m\le2\right)\)
Vậy hàm số đồng biến trên khoảng (1;3) \(\Leftrightarrow m\in\left(-\infty;2\right)\)




Chọn D.
Ta có: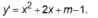
Hàm số đồng biến trên ℝ