Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét rằng khi thay x=0 vào hệ bất phương trình, ta được :
\(\begin{cases}0-1<3-0\\m.0+1>0\end{cases}\) \(\Leftrightarrow\begin{cases}-1<3\\1>0\end{cases}\)
Hệ này luôn đúng với mọi \(m\in R\)
Vậy với mọi \(m\in R\) , hệ bất phương trình đã cho luôn có ít nhất một nghiệm (x=0).
Do đó với \(m\in R\) hệ bất phương trình đã cho luôn có nghiệm

\(\begin{cases}x^2+7x-8\le0\\a^2x+1>3+\left(3a-2\right)x\end{cases}\) (1)
\(\Leftrightarrow\) \(\begin{cases}x^2+7x-8\le0\\\left(a^2-3a+2\right)x>2\end{cases}\)
ta đặt
\(x^2+7x-8\le0\) (a)
\(\left(a^2-3a+2\right)x>2\) (b)
(1) Vô nghiệm khi và chỉ khi T(a)\(\cap\)T(b) = \(\varnothing\)
Dễ thấy T(a) = \(\left[-8;1\right]\). Đặt m:=\(a^2-3a+2\), xét các trường hợp sau :
- Nếu a=1 hoặc a=2 thì
\(\left(a^2-3a+2\right)x>2\) \(\Leftrightarrow\) 0.x > 2 \(\Rightarrow\) T ( b) = \(\varnothing\) nên (1) vô nghiệm
- Nếu \(a\in\left(-\infty;1\right)\cup\left(2;+\infty\right):=\)(*) thì m >0 nên T(b) có nghiệm \(x>\frac{2}{m}\) Ta có :
T(a)\(\cap\) T(b) = \(\varnothing\) \(\Leftrightarrow\) \(\frac{2}{m}\ge1\)
\(\Leftrightarrow\) \(2\ge m=a^2-3a+2\) ( do m>0 trong (*)
\(\Leftrightarrow\) \(a^2-3a\le0\) \(\Leftrightarrow\) \(0\le a\le3\)
Kết hợp với điều kiện \(a\in\)(*) được \(0\le a<1\) hoặc 2<a\(\le\)3
- Nếu \(a\in\)(1;2) thì m<0 nên T(b) có nghiệm \(x<\frac{2}{m}\) Ta có T(a)\(\cap\) T(b) = \(\varnothing\) \(\Leftrightarrow\) \(\frac{2}{m}\le-8\)
\(\Leftrightarrow\) \(2\ge-8m=-8\left(a^2-3a+2\right)\) (do m<0 trong (1;2)
\(\Leftrightarrow\) \(4a^2-12a+9\ge0\) \(\Leftrightarrow\) \(\left(2a-3\right)^2\ge0\) luôn đúng
Vậy với \(a\in\)(1;2) thì (1) vô nghiệm. Tóm lại ta được 0\(\le a\le\)3 là các giá trị cần tìm

câu b
- Xét m = 0.
Phương trình trở thành: \(-10x-5=0\)\(\Leftrightarrow x=\dfrac{-1}{2}\) .
Khi m = 0 phương trình có nghiệm \(x=\dfrac{1}{2}\) (loại).
Xét \(m\ne0\) (1)
Phương trình vô nghiệm: => \(\Delta< 0\) \(\Rightarrow25+5m< 0\Rightarrow m< \dfrac{-25}{5}=-5\) (2)
Kết hợp với điều kiện (1) suy ra với \(m>-5\) thì phương trình vô nghiệm.
Làm lại:
a)
\(5x^2-x+m\le0\)(a)
để (a)vô nghiệm \(\Rightarrow5x^2-x+m=0\) phải vô nghiệm => \(\Delta=1-20m< 0\Rightarrow m>\dfrac{1}{20}\)
b)\(mx^2-10x-5\ge0\left(b\right)\)
Để b vô nghiệm cần
(1) \("a"\ne0\Rightarrow m\ne0\)
(2) \("a"< 0\Rightarrow m< 0\)
(3) \(\left[{}\begin{matrix}\Delta\\\Delta'\end{matrix}\right.< 0\Rightarrow\)\(5^2+5m< 0\Rightarrow m< \dfrac{-25}{5}=-5\)
(1)&(2)(3)Kết luận \(m< -5\)

Lười làm lắm cứ xét từng khoản là được
Đầu tiên giải bất thứ nhất
Ở bất thứ 2 xét 2 trường hợp
- TH 1: \(m\le0\)
- TH2: \(m>0\)
+ \(\hept{\begin{cases}m-x^2>0\\x+m< 0\end{cases}}\)
+\(\hept{\begin{cases}m-x^2< 0\\x+m>0\end{cases}}\)
Chọn B
+ Bpt: 3x+ 5 ≥ x- 1 hay 2x ≥ - 6
Suy ra: x ≥ - 3
Tập nghiệm S1= [-3; + ∞)
+ Bpt : (x+ 2) 2 ≤ ( x-1) 2+ 9
Hay 4x+4 ≤ -2x+ 1+ 9
Suy ra: 6x ≤ 6
Do đó; x ≤ 1 và S2= ( -∞; 1]
Suy ra :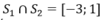
+ Xét bpt : mx+ 1> ( m-2) x+ m
Tương đương : 2x> m-1
Hay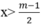
từ đó tập nghiệm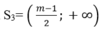
+ Để hệ bpt vô nghiệm khi và chỉ khi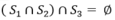
Suy ra :