Tập xác định của hàm số y = l o g ( x...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

20 tháng 2 2019

Tập xác định của hàm số y = l o g ( x 2 - 1 ) là

A. - ∞ ; - 1 ∪ 1 + ∞

B. - ∞ ; 1

C. 1 + ∞

D. (-1;1)

1

CM

Cao Minh Tâm

20 tháng 2 2019

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NH

Nguyễn Hoàng Bảo Khang

2 tháng 10 2015

Cho hàm số \(y=\frac{ax^2-bx}{x-1}\)

Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm \(A\left(-1;\frac{5}{2}\right)\)và tiếp tuyến của (C) tại điểm O(0;0) có hệ số góc bằng -3

1

NT

nguyen thi khanh hoa

2 tháng 10 2015

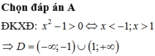
vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)

ta tính y' có:

\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)

vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)

thay b=-3 vào (*) ta tìm được a=-2

vậy a=-2;b=-3

NH

Nguyễn Hoàng Bảo Khang

3 tháng 10 2015

Cho hàm số \(y=\frac{ax^2-bx}{x-1}\)

Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm \(A\left(-1;\frac{5}{2}\right)\)và tiếp tuyến của (C) tại điểm O(0;0) có hệ số góc bằng -3

1

NT

nguyen thi khanh hoa

3 tháng 10 2015

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)

vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3

ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2

vậy ta tìm đc a và b

NN

Nguyễn Như Ý

1 tháng 2 2016

câu 1 :Gía trị x=1 có phải là nghiệm của phương trình hya không?Vì sao?

câu 2:Tìm điều kiện xác định của mỗi phương trình sau:

a)\(\frac{x}{x-1}\)=\(\frac{x+4}{x+1}\)

b)\(\frac{3}{x-2}\)=\(\frac{2x+3}{x-2}\)

9

DM

Đặng Minh Triều

1 tháng 2 2016

a) ĐK: x-1 khác 0 và x+1 khác 0

<=> x khác 1 và x khác -1

b) ĐK: x-2 khác 0

<=> x khác 2

NN

Nguyễn Như Ý

1 tháng 2 2016

à thui câu 1 k cần lm lm hộ câu 2 nha

NH

Nguyễn Hoàng Bảo Khang

4 tháng 10 2015

Cho hàm số \(f\left(x\right)=x^3-3mx^2+3\left(2m-1\right)x+1\)

Chứng minh rằng với mọi giá trị của m, đồ thị (\(C_m\)) của hàm số đã cho và đường thẳng \(y=2mx-4m+3\) luôn có 1 điểm chung cố định

17

NT

nguyen thi khanh hoa

5 tháng 10 2015

hoành độ giao điểm là nghiệm của pt

\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)

giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau

\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)

ta đc điều phải cm

N

Nguyễn

27 tháng 10 2019

.

NP

Nguyen Phuong Linh

17 tháng 3 2016

Cho hàm số f(x) xác định với mọi x

Biết f(x) + 3f(\(\frac{1}{x}\))= x²

Thì f(2)=...

2

NH

Nguyễn Hoàng Việt

11 tháng 1 2017

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:

\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)

Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)

Tìm được \(f\left(2\right)=\frac{-13}{32}\)

HL

Hoàng Lê Bảo Ngọc

12 tháng 1 2017

Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)

Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)

\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)

Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)

\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)

Vậy f(2) = -13/32

NM

ngo mai trang

30 tháng 9 2015

tìm giá trị nhỏ nhất và lớn nhất của hàm số sau

\(y=\frac{x^2-x+1}{x-1}\) trên \(\left[-2;\frac{1}{2}\right]\)

1

NT

nguyen thi khanh hoa

30 tháng 9 2015

ta tính \(y'=\frac{x\left(x-2\right)}{\left(x-1\right)^2}\)

giải pt y'=0

ta có \(x\left(x-2\right)=0\) suy ra x=0 hoặc x=2

bảng bt

x y' y -2 0 1/2 2 0 0 + - -7/3 -1 -3/2

hàm số đạt giá trị lớn nhất =-1 tại x=0, đạt giá trị nhỏ nhất =-7/3 tại x=-2

NM

ngo mai trang

1 tháng 10 2015

cho hàm số \(y=x^3-3x-1\)

viết phương trình tiếp tuyến của hàm số tại điểm A(0;-1)

1

NT

nguyen thi khanh hoa

1 tháng 10 2015

đây là dạng toán viết phương trình tiếp tuyến tại một điểm A(a,b)

ta là như sau:

bước 1: tính y'

bước 2: tính y'(a)

bước 3: áp dụng công thức y=y'(a)(x-a)+b

áp dụng vào bài trên ta có

\(y'=3x^2-3\)

\(y'\left(0\right)=-3\)

vậy phương trình tiếp tuyến của đồ thị có dạng

\(y=-3\left(x-0\right)+\left(-1\right)=-3x-1\)

NM

ngo mai trang

1 tháng 10 2015

cho hàm số \(y=x^3+1\)

viết phương trình tiếp tuyến của hàm số biết tiếp tuyến vuông góc với đường thẳng \(y=-3x+1\)

1

NT

nguyen thi khanh hoa

1 tháng 10 2015

ta tính \(y'=3x^2\)

để tiếp tuyến của đồ thị hàm số song song với đường thẳng \(y=-3x+1\) thì \(y'\left(x_0\right)=\frac{-1}{-3}=\frac{1}{3}\) giả pt suy ra đc \(x_0=\pm\frac{1}{3}\)

TH1: \(x_0=\frac{1}{3}\) suy ra \(y_0=\frac{1}{27}+1=\frac{28}{27}\)

vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x-\frac{1}{3}\right)+\frac{28}{27}=\frac{1}{3}x+\frac{25}{27}\)

TH2:\(x_0=-\frac{1}{3}\) suy ra \(y_0=-\frac{1}{27}+1=\frac{26}{27}\)

vậy phương trình tiếp tuyến cần tìm là \(y=\frac{1}{3}\left(x+\frac{1}{3}\right)+\frac{26}{27}=\frac{1}{3}x+\frac{29}{27}\)

DT

Đinh Tuấn Việt

21 tháng 3 2016

Cho hàm số \(y=f\left(x\right)=ax+b\) với a khác 0

Biết \(f\left(1\right).f\left(-1\right)=\left(a+b\right)^2\)

Khi đó \(5-3a-3b=...\)

7

TT

Trần Thùy Dung

21 tháng 3 2016

Ta có:

\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)

\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)

\(\Rightarrow-a+b=a+b\)

\(\Rightarrow a=-a\)

\(a\ne0\) thì làm sao có a thỏa mãn được?

DT

Đinh Tuấn Việt

21 tháng 3 2016

Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.

DT

Đặng Thị Cẩm Tú

27 tháng 4 2016

1/ a) Hãy xác định tập hợp sau bằng cách chỉ rõ tính đặc trưng của các phần tử

A=\(\left\{1;7;13;19;25;31;37\right\}\)

b) Tính giá trị biểu thức sau

B=\(\left(3\frac{10}{99}+4\frac{11}{99}-5\frac{8}{299}\right).\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\)

mí bn oj gjup mik vs nka

14

PN

Phạm Nguyễn Tất Đạt

27 tháng 4 2016

câu b:(3/10/99+4/10/99-5/8/299)*(1/2-1/3-1/6)

=(3/10/99+4/10/99-5/8/299)*(3/6-2/6-1/6)

=(3/10/99+4/10/99-5/8/299)*0

=0

PN

Phạm Nguyễn Tất Đạt

27 tháng 4 2016

(xEN*/7<=x+6<=43,x-1 chia hết cho 6)(tui nghĩ là vậy )