Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
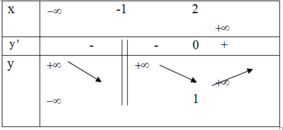
Dựa vào bảng biến thiên, ta có lim x → 1 y = ± ∞ ⇒ x = − 1 là TCĐ của đồ thị hàm số
Và lim x → ± ∞ y = + ∞ suy ra hàm số không có tiệm cận ngang

Đáp án C
f ' x > 0 ⇔ 1 < x < 2 ⇒ hàm số đồng biến trên khoảng (1;2)

a)Q(x) = 6x^3 - x^2 +1 -2x^3 +3x^4 -4x^3 -2x^4 +4x^2
\(=\left(3x^4-2x^4\right)+\left(6x^3-2x^3-4x^3\right)+\left(4x^2-x^2\right)+1\)
\(Q\left(x\right)=x^4+3x^2+1\)
b) \(Q\left(3\right)=3^4+3.3^2+1=81+27+1=109\)
\(Q\left(-3\right)=\left(-3\right)^4+3.\left(-3\right)^2+1=81+27+1=109\)

Đáp án C
Ta có bảng biến thiên của hàm số y = f x như sau:
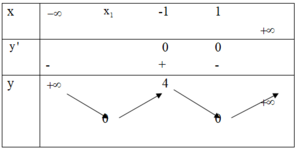
Từ bảng biến thiên suy ra f x = m với m ∈ 0 ; 4 có 4 nghiệm

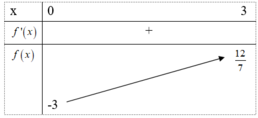
ở đây:
Cho đa thức Q(x) = 6x3 - x2 +1 -2x3 +3x4 -4x3 -2x4 +4x2
a) Thu gọn và sắp xếp các hạng tử của đa thức Q(x) theo lũy thừa giảm dần của biến
b) Tính Q(3) ; Q(-3)
LIKE~~~~

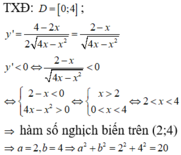

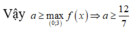

Đáp án đúng : A