Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{SS}\) \(=\dfrac{U}{I'}=\dfrac{12}{1,6}=7,5\left(ÔM\right)\)
\(R_{NT}=\dfrac{U}{I}=\dfrac{12}{0,3}=40\left(ÔM\right)\)
Ta có: \(R_{NT}.R_{SS}=\left(R_1+R_2\right).\dfrac{R_1.R_2}{R_1+R_2}=\) \(R_1.R_2=40.7,5=300\left(ÔM\right)\)
mạch nt: \(R_1+R_2=40\Rightarrow R_2=40-R_1\)
\(\Rightarrow\)\(R_1.\left(40-R_1\right)=300\Rightarrow R_1=30\) hoặc \(R_1=10\)
Vậy: \(TH_1:R_1=30;R_2=10\)
\(TH_2:R_1=10;R_2=30\)

Khi R1 mắc nối tiếp với R2 thì: 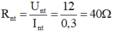 ↔ R1 + R2 = 40Ω (1)
↔ R1 + R2 = 40Ω (1)
Khi R1 mắc song song với R2 thì:
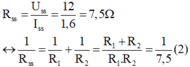
Thay (1) vào (2) ta được R1.R2 = 300
Ta có: R2 = 40 – R1 → R1.(40 – R1) = 300 ↔ - R12 + 40R1 – 300 = 0 (*)
Giải (*) ta được: R1 = 30Ω; R2 = 10Ω hoặc R1 = 10Ω; R2 = 30Ω.

ta có:
khi mắc chúng nối tiếp:
\(R_1+R_2=R=\frac{U}{I}\)
\(\Leftrightarrow R_1+R_2=40\)
\(\Rightarrow R_2=40-R_1\)
khi mắc chúng song song:
\(\frac{R_1R_2}{R_1+R_2}=R=\frac{U}{I'}\)
\(\Leftrightarrow\frac{R_1\left(40-R_1\right)}{R_1+40-R_1}=7,5\)
\(\Leftrightarrow\frac{40R_1-R_1^2}{40}=7,5\)
\(\Leftrightarrow40R_1-R_1^2=300\)
\(\Rightarrow-R_1^2+40R_1-300=0\)
giải phương trình bậc hai ở trên ta được:
R1=30Ω\(\Rightarrow R_2=10\Omega\)
R1=10Ω\(\Rightarrow R_2=30\Omega\)

Khi mắc nối tiếp:
\(R_{tđ}=R_1+R_2=\dfrac{U}{I}=\dfrac{24}{0,6}=40\left(\Omega\right)\left(1\right)\)
Khi mắc song song:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12}{1,6}=\dfrac{15}{2}\Rightarrow R_1.R_2=\dfrac{15}{2}.40=300\left(\Omega\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}R_1+R_2=40\left(\Omega\right)\\R_1.R_2=300\left(\Omega\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300}{R_2}+R_2=40\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\dfrac{300+R_2^2}{R_2}=40\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}R_1=\dfrac{300}{R_2}\\\left(R_2-30\right)\left(R_2-10\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}R_1=10\left(\Omega\right)\\R_2=30\left(\Omega\right)\end{matrix}\right.\\\left\{{}\begin{matrix}R_1=30\left(\Omega\right)\\R_2=10\left(\Omega\right)\end{matrix}\right.\end{matrix}\right.\)

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

R 1 nối tiếp R 2 nên điện trở tương đương của mạch lúc này là:
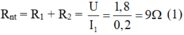
R 1 song song với R 2 nên điện trở tương đương của mạch lúc này là:
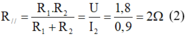
Lấy (1) nhân với (2) theo vế ta được
R
1
.
R
2
= 18 → 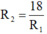 (3)
(3)
Thay (3) vào (1), ta được: R 12 - 9 R 1 + 18 = 0
Giải phương trình, ta có: R 1 = 3Ω; R 2 = 6Ω hay R 1 = 6Ω; R 2 = 3Ω

- Điện trở tương đương của mạch khi mắc R1 nối tiếp với R2 là :
\(Rnt=\frac{Unt}{Int}=\frac{6}{0,24}=25\left(ôm\right)\)
hay R1 + R2 = 25 (Ω) (1)
- Điện trở tương đương của mạch khi mắc R1 song song với R2 là :
\(R_{ss}=\frac{U_{ss}}{I_{ss}}=\frac{6}{1}=1\)(Ω)
hay \(\frac{R_1.R_2}{R_1+R_2}=6\left(ôm\right)\)
-> R1.R2=6.(R1+R2)=6.25 hay R1.R2=150 (Ω) (2)
Giải hệ phương trình (1) và (2) ta được :
\(\begin{cases}R_1=15\left(\Omega\right),R_2=10\left(\Omega\right)\\R_1=10\left(\Omega\right),R_2=15\left(\Omega\right)\end{cases}\)
Vậy nếu R1=15(Ω) thì R2=10(Ω) , R1=10(Ω) thì R2=15(Ω)
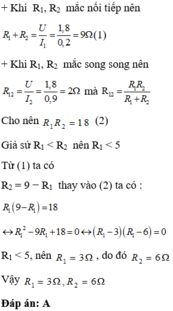
R 1 + R 2 = U / I = 40 ( R 1 . R 2 ) / ( R 1 + R 2 ) = U / I ’ = 7 , 5
Giải hệ pt theo R 1 ; R 2 ta được R 1 = 30 ; R 2 = 10
Hoặc R 1 = 10 ; R 2 = 30