Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Phân tích
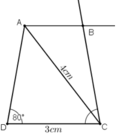
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên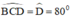 
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn
+ Dựng cung tròn tâm C, bán kí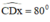
nh 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn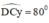 
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có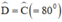 
nên là hình thang cân.
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm,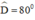 
nên thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.
Hình vẽ ;
A D B C E 60 o
a, Chứng minh tứ giác ABCD là hình thang cân .
Xét tam giác ADC ( góc ACD = 90 độ do AC\(⊥\)CD-gt) ta có :
\(\widehat{D}+\widehat{CAD}=90^o\)
\(\Rightarrow\widehat{CAD}=90^o-\widehat{D}=90^o-60^o=30^o\)
mà \(\widehat{CAD}=\widehat{BAC}\left(gt\right)\Rightarrow\widehat{BAC}=30^o\)
Ta có : \(\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=30^o+30^o=60^o\)
Xét hình thang ABCD , ta có :
\(\widehat{BAD}=\widehat{D}=60^o\)
\(\Rightarrow\)tứ giác ABCD là hình thang cân.
b, Tính AD.
Kéo dài AB và DC cắt nhau tại E .
Xét tam giác AED , ta có : \(\widehat{BAC}=\widehat{CAD}\left(gt\right)\)
\(AC⊥CD\)(gt)
=> tam giác AED là tam giác cân .
mà góc D = 60 độ (gt)
=> tam giác AED là tam giác đều
=>\(\hept{\begin{cases}AB=CD=\frac{1}{2}AD\left(1\right)\\CE=CD\end{cases}}\)
Xét tam giác ADE , ta có :
BC//AD( do ABCD là hình thang )
CE=CD( cmt)
=> BC là đường trung bình của tam giác ADE
=>\(BC=\frac{1}{2}AD\left(2\right)\)
Từ (1) và (2) => BC=CD=AB=\(\frac{1}{2}.AD\)
Theo giả thiết , ta có :
AB+BC+CD+AD=20
=>\(\frac{1}{2}AD+\frac{1}{2}AD+\frac{1}{2}AD+AD=20\)
=>\(\frac{5}{2}AD=20\Rightarrow AD=8\left(cm\right)\)
Nên nhớ hình vẽ chỉ mang tính minh họa cho bài làm nên ko được đẹp lắm đâu các bạn thông cảm cho.
Trong bài mk làm hơi tắt có j hk hiểu nhắn tin hỏi mk .
A B C D
a)
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\frac{C+D}{2}+C+D=360^o\)
\(\Leftrightarrow\frac{3\left(C+D\right)}{2}=360^o\)
\(\Leftrightarrow3\left(C+D\right)=720^o\)
\(\Leftrightarrow C+D=240^o\)
\(\Leftrightarrow A+B=120\)
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên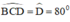
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn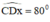
+ Dựng cung tròn tâm C, bán kính 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn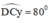
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có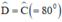
nên là hình thang cân.
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm,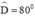
nên thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.