Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

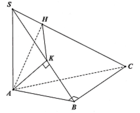
Ta có A K ⊥ S C A K ⊥ α A K ⊥ B C B C ⊥ S A B
Suy ra A K ⊥ S B C ⇒ A K ⊥ S B .
Vì ∆ S A B vuông cân tại A nên K là trung điểm của SB. Ta có
V S . A H K V S . A B C = S A . S K . S H S A . S B . S C = S H 2 S C
Ta có
A V = A B 2 + B C 2 = 2 a S V = A C 2 + S A 2 = a 5 .
Khi đó S H S C = S H . S C S C 2 = S A 2 S C 2 = 1 5
Suy ra V S . A H K V S . A B C = S H 2 S C = 1 10
Mặt khác V S . A B C = 1 3 S A . 1 2 A B . B C = a 3 3 6 Vậy V S . A H K = a 3 3 60
Đáp án C

Đáp án C
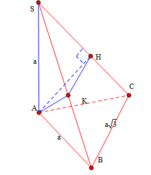
A C = A B 2 + B C 2 = a 2 + 3 a 2 = 2 a
S C = S A 2 + A C 2 = a 2 + 4 a 2 = a 5
S H = S A 2 S C = a 2 a 5 = a 5
S B = S A 2 + A B 2 = a 2 + a 2 = a 2
Δ S H K ~ Δ S B C ⇒ S H S B = S K S C ⇒ S K = S H . S C S B = a . a 5 5 . a 2 = a 2
⇒ V S . A H K V S . A B C = S H S C S K S B = a 5 a 5 a 2 a 2 = 1 10 ⇒ V S . A H K = 1 10 V S . A B C = 1 3 S A . d t A B C = 1 10 . 1 3 a . 1 2 a . a 3 = a 3 3 60

Đáp án D
Phương pháp giải:
Xác định tâm mặt cầu ngoại tiếp đi qua các đỉnh của khối chóp bằng phương pháp dựng hình, từ đó dựa vào tính toán xác định bán kính – thể tích mặt cầu.
Lời giải:

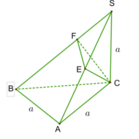


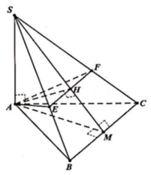
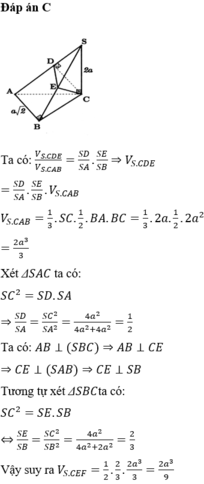
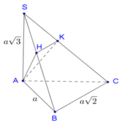


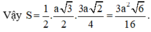

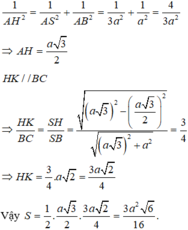
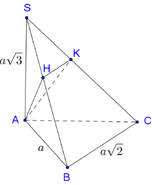
Ta có:
S B = a 2 + b 2 = a 2 A C 2 = a 2 + 3 a 2 = 4 a 2 ⇒ S C = a 2 + 4 a 2 = a 5 S K = S A 2 S B = a 2 a 2 = a 2 S H = S A 2 S C = a 2 a 5 = a 5 V S . A H K V S . A B C = S K . S H S B . S C = 1 2 . 1 5 = 1 10 ⇒ V S . A H K = 1 10 V S . A B C = 1 60 S A . B A . B C = 1 60 3 a 3
Đáp án cần chọn là C