Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
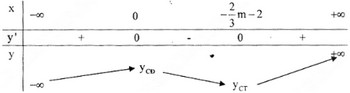
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53

Lời giải
khảo sát
TXD mọi x
y' =3x^2 -6x =3x(x-2)
y' =0 => x= 0 hoặc x=2
y'' =6x-6
y''(0) =-6 <0 hàm đạt cực đại tại x=0
y''(2) =6 >0 hàm đạt cực tiểu tại x =2
y'' =0 => x=1 hàm có điểm uốn tại x=1
hàm đi từ - vc--> +vc đi góc (III) lên (IV)
Vẽ đồ thị
Các điểm quan trọng
cực đại A(0,0)
cực tiểu B(2,-4)
uốn C(1,-2)
Các điểm phụ trọng
giao với trục hoành E(0,0); \(F\left(3;0\right)\)
Giao với trục tung: \(A\left(0,0\right)\)
Đồ thị

b)
nhìn vào đồ thị số y=x^3 -3x^2
Hàm số x^3 -3x^2 -m có 3 nghiệm phân biệt
khi 0<m<-4

a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
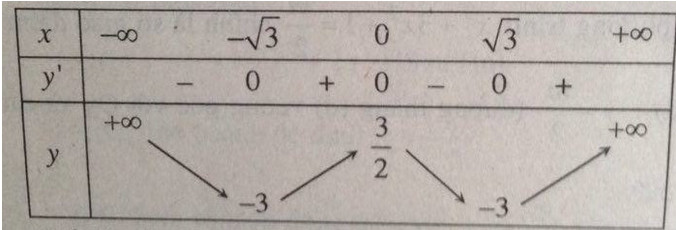
Đồ thị hàm số:
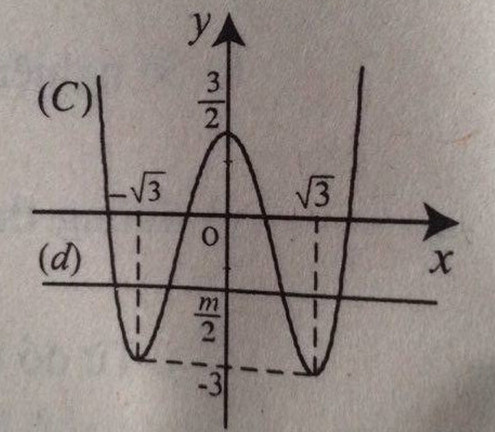
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
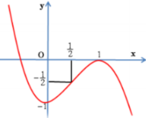






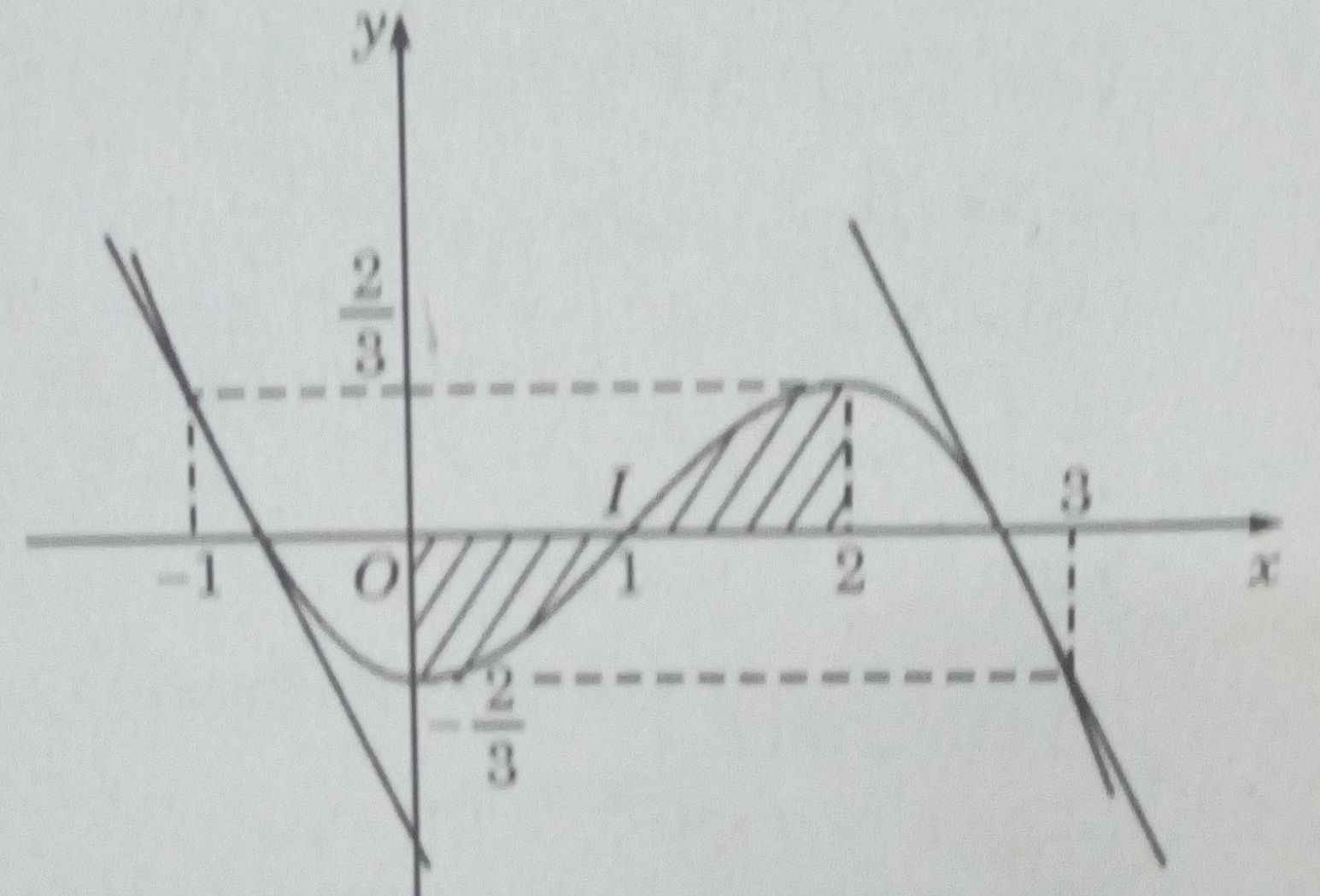

Đáp án D