Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) con số này cho biết cứ 1m dây bằng Đồng có tiết diện 1m2 này có điện trở là 0,5.10-6
b) R= P.( L/S) = 0.5.10-6 .. (20/0.4.10-6 ) = 25 ôm ( S = 0.4.10-6) là vì đổi về mm2 nha bạn

a)con số 25Ω-1A trên biến trở cho biết điện trở lớn nhất và cường độ dòng điện lớn nhất có thể dặt vào hai đầu diện trở.Hiệu điện thế lớn nhất có thể đặt vào hai đầu biến trở là:
\(U_{max}=I_{max}R_{max}=25V\)
b) ta có:
\(R=\rho\frac{l}{S}\)
\(\Leftrightarrow25=11.10^{-6}\frac{24}{S}\Rightarrow S=1,056.10^{-5}m^2\)
a)con số 25 ôm-1A cho biết điện trở định mức và cường độ dòng điện định mức của biến trở đó. theo định luật ôm thì R=U/I => U=I*R=1*25=25V
b) Tiết diện của dây dẫn dùng làm biến trở là:
R=rô*l/S =>S=rô*l/R=11*10^-6/24=1,056*10^-5
Đáp số: a)U=25V
b)S=1,056*10^-5

- Tính được điện trở cuả dây xoắn là:
\(R=p\frac{l}{s}=5,4.10^{-4}.\frac{10}{0,2.10^{-6}}=27\left(\Omega\right)\)
- Cường độ dòng điện qua bếp : I = \(I=\frac{U}{R}=\frac{220}{27}=8,14\left(A\right)\)
- Tính được nhiệt lượng cần cho nước đã cho đến sôi(Q hữu ích):
Q = cm(t2 – t1) = 4200 J/kg.K.2kg.(100 -15) = 714000J
- Do bếp có hiệu suất nên nhiệt lượng bếp phải cấp :
\(H=\frac{Qi}{Q}.100\%\)80% =>\(Q=\frac{Qi.100\%}{H}=\frac{71400.100\%}{80\%}=892500\left(J\right)\)
- Nhiệt lượng này do điện năng chuyển thành từ dây xoắn. Vậy thời gian cần thiết cho nước sôi :
Q = A = U.I.t = >t = \(\frac{Q}{UI}=\frac{892500}{220.8,14}=497,8\left(s\right)\) = 8,3(phút)
cái đáp án điện trở có phải sai rồi không ? Tôi bấm máy nó lại ra 27000 ohm ấy

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m

1/ Điện trở của một dây dẫn không phụ thuộc vào khối lượng của dây dẫn.
2/ Hiệu điện thế đặt vào điện trở \(R_2\) là: \(U_2=I_2.R_2=2.6=12V\)
Mà \(R_1\) mắc song song với \(R_2\) nên \(U_{tm}=U_1=U_2\)
\(\rightarrow U_1=U_2=12V\)
Áp dụng định luật \(\Omega\): \(I_1=\frac{U_1}{R_1}=\frac{12}{4}=3A\)

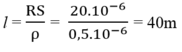
→ Đáp án C