
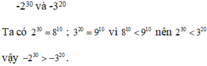
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

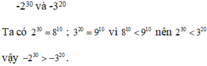

2300 VÀ 3200
2300 = ( 23)100 = 8100
3200 = ( 32)100 = 9100
VÌ 9100 > 8100 => 2300 < 3200
NHỮNG CON KHÁC BẠ ĐƯA VỀ CÙNG CƠ SỐ SAU ĐÓ SO SÁNH MŨ SỐ LÀ ĐC

a) Ta có: \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
b) Ta có: \(2^{31}=\left(2\frac{31}{21}\right)^{21}=2,7822^{21}< 3^{21}\Rightarrow2^{31}< 3^{21}\)
c) Ta có: \(3^{30}=\left(3^3\right)^{10}=27^{10}\)
\(2^{30}=\left(2^3\right)^{10}=8^{10}\)
\(4^{30}=\left(4^3\right)^{10}=64^{10}\)
Lại có: \(3.24^{10}=2.24^{10}+24^{10}\Rightarrow24^{10}< 27^{10}\left(1\right)\)
\(2.24^{10}< 48^{10}< 64^{10}\left(2\right)\)
Từ 1,2 => \(24^{10}+2.24^{10}< 27^{10}+64^{10}\Rightarrow3.24^{10}< 8^{10}+27^{10}+64^{10}\)
\(\Rightarrow3.24^{10}< 3^{30}+2^{30}+4^{30}\)

\(2^0+2^1+2^2+2^3+...+2^{50}=1+2+2.2+2^2.2+...+2^{49}.2\)
\(=1+2\left(1+2+2^2+2^3+...+2^{49}\right)\)
\(=1+2\left(2^{50}-1\right)\)
\(=1+2^{51}-2\)
\(=2^{51}-1< 2^{51}\)
Vậy \(2^0+2^1+2^2+2^3+...+2^{50}< 2^{51}\)
Ý trc mình ko biết sorry bạn nhiều
T i c k cho mình nha mình mới có 4 điểm, thanks


a) \(2^{24}=2^{3.8}=8^8\) \(3^{16}=3^{2.8}=9^8\)
Do \(8^8< 9^8\)=> \(2^{24}< 3^{16}\)
b) \(3^{200}=3^{2.100}=9^{100}\); \(2^{300}=2^{3.100}=8^{100}\)
Do \(9^{100}>8^{100}\)=> \(3^{200}>2^{300}\)
c) \(7^{20}=7^{4.5}=2401^5>71^5\)
Vậy \(7^{20}>71^5\)
d) \(\left(-2\right)^{30}=2^{30}=2^{3.10}=8^{10}\); \(\left(-3\right)^{20}=3^{20}=3^{2.10}=9^{10}\)
Do \(8^{10}< 9^{10}\)nên \(\left(-2\right)^{30}< \left(-3\right)^{20}\)
e) \(\left(-5\right)^9< 0\); \(\left(-2\right)^{18}=2^{18}>0\)
Vậy \(\left(-5\right)^9< \left(-2\right)^{18}\)


Ta có :
1) 45^10 . 5^30= (5.9)^10 . 5^30 = 5^10 . 5^30 . 9^10 = 5^40 . 3^20 = 25^20 . 3^20=75^20
2)\(\sqrt{40+2}=\sqrt{42}<\sqrt{49}=7=6+1=\sqrt{36}+\sqrt{1}<\sqrt{40}+\sqrt{2}\)
Vậy \(\sqrt{40+2}<\sqrt{40}+\sqrt{2}\)
3)\(Cho\frac{x}{3}=\frac{y}{4}=k\Rightarrow x=3k;y=4k\)
Ta lại có:
\(xy=12\Rightarrow3k.4k=12\)
\(12.k^2=12\Rightarrow k^2=1\Rightarrow k=1:-1\)
\(Vơik=1\Rightarrow x=1.3=3;y=1.4=4\)
\(k=-1\Rightarrow x=-1.3=-3;y=-1.4=-4\)

+)\(8^2=\left(2^3\right)^2=2^6\)
+)\(3^{200}=3^{2.100}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=2^{3.100}=\left(2^3\right)^{100}=8^{100}\)
Vì \(9>8\Rightarrow9^{100}>8^{100}\)hay \(3^{200}>2^{300}\)
+)\(9^{20}=\left(3^2\right)^{20}=3^{40}\)
\(27^{13}=\left(3^3\right)^{13}=3^{39}\)
Vì \(40>39\Rightarrow3^{40}>3^{39}\)hay \(9^{20}>27^{13}\)
+)\(10^{20}=10^{2.10}=\left(10^2\right)^{10}=100^{10}\)
\(2^{100}=2^{10.10}=\left(2^{10}\right)^{10}=1024^{10}\)
Vì \(100< 1024\Rightarrow100^{10}< 1024^{10}\)hay \(10^{20}< 2^{100}\)
+)\(2^{161}=2^{4.40+1}=\left(2^4\right)^{40}.2=16^{40}.2\)
Vì \(13< 16\Rightarrow13^{40}< 16^{40}\)\(\Rightarrow13^{40}< 2^{161}\)
