K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 7 2016
a) \(A=\frac{\left(a^3+a^2\right)+\left(a^2-1\right)}{\left(a^3+a^2\right)+\left(a^2+a\right)+\left(a+1\right)}=\frac{a^2.\left(a+1\right)+\left(a+1\right).\left(a+1\right)}{a^2.\left(a+1\right)+a.\left(a+1\right)+\left(a+1\right)}=\frac{\left(a+1\right).\left(a^2+a-1\right)}{\left(a+1\right).\left(a^2+a+1\right)} \)\(=\frac{a^2+a-1}{a^2+a+1}\)
b) ﴿ Gọi ƯCLN ﴾ a2 + a - 1 ; a2 + a + 1 ) = d
\(\Rightarrow\begin{cases}a^2+a-1⋮d\\a^2+a+1⋮d\end{cases}\)
\(\Rightarrow\left(a^2+a+1\right)-\left(a^2+a-1\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\inƯ\left(2\right)=\left\{1;2\right\}\)
Vậy d = 1 hoặc d = 2
Nhận xét: \(a^2+a-1=a.\left(a+1\right)-1\)
Với số nguyên a ta có \(a\left(a-1\right)\) là tích 2 số nguyên liên tiếp
=> \(a\left(a-1\right)⋮2\) => \(a\left(a-1\right)-1\) lẻ => \(a^2+a-1\) lẻ
=> d \(\ne\) 2
Vậy d = 1
Vì d = 1 => A là phân số tối giản ( đpcm )
MD
13 tháng 11 2016
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các bài toán hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
29 tháng 10 2016
Bài 1:
Có: n2 + n = n(n+1)
Xét: Nếu n lẻ thì n+1 chẵn => n(n+1) chia hết cho 2 (1)
Nếu n chẵn thì n chẵn => n(n+1) chia hết cho 2 (2)
Từ (1) và (2) => n2 + n là hợp số
Bài 2:
a) M = 1 + 32 + 34 + ... + 398
=> 9M = 32 + 34 + ... + 3100
=> 9M - M = 3100 - 1
=> M = \(\frac{3^{100}-1}{8}\)
b) M = 1 + 32 + 34 + ... + 398
= (1+32) + (34+36) + ... + (396+398)
= 10 + 34(1+32) + ... + 396(1+32)
= 10(34+...+396) \(⋮\) 10
29 tháng 10 2016
Bài 2:
a) \(M=1+3^2+3^4+3^6+3^8+...+3^{98}\)
\(\Rightarrow9M=3^2+3^4+3^6+...+3^{100}\)
\(\Rightarrow9M-M=\left(3^2+3^4+3^6+...+3^{100}\right)-\left(1+3^2+3^4+...+3^{98}\right)\)
\(\Rightarrow8M=3^{100}-1\)
\(\Rightarrow M=\frac{3^{100}-1}{8}\)
b) \(M=1+3^2+3^4+...+3^{98}\)
\(\Rightarrow M=\left(1+3^2\right)+\left(3^4+3^6\right)+...+\left(3^{96}+3^{98}\right)\)
\(\Rightarrow M=\left(1+9\right)+3^4\left(1+3^2\right)+...+3^{96}\left(1+3^2\right)\)
\(\Rightarrow M=10+3^4.10+3^{96}.10\)
\(\Rightarrow M=\left(1+3^4+3^{96}\right).10⋮10\)
\(\Rightarrow M⋮10\)
11 tháng 7 2016
Bài 1:Tính nhanh
a,149+152+257+138 = 149 + 257 + ( 152 + 138 ) = 696
b,12.19.25 = ( 12.25 ).19 = 5700
c,79.37+79.18-55.78
= 79.(37+18) -55.78
= 79.55-55.78
=55.(79-78)
=55
Bài 2:Tìm x biết:
a,83+7.(25-x)=167
7. (25-x)=167-83
7. (25-x)=84
25-x=84:7
25-x=12
x=13
b,149-9.(x+12)=14
9.(x+12)=149-14
9.(x+12)=135
x+12= 135:9
x+12=15
x = 3
c,(x+9). (x+7)=143
\(\Leftrightarrow x+9=143\) hoặc \(x+7=143\)
\(\Leftrightarrow x=134\) hoặc \(x=136\)
NA
11 tháng 7 2016
Bài 1:Tính nhanh
a,149+152+257+138
= (152 + 138) + (149 + 257)
= 290 + 406 = 696
b,12.19.25
= (25.12) .19
= 300.19 = 5700
c,79.37 + 79.18 - 55.78
= 79.(37 + 18) - 55.78
= 79.55 - 55.78
= 55.(79 - 78)
= 55.1 = 55
Bài 2:Tìm x biết:
a,83 + 7.(25 - x) = 167
7.(25 - x) = 167 - 83
7.(25 - x) = 84
25 - x = 84 : 7
25 - x = 12
x = 25 - 12 = 13
b,149 - 9.(x + 12) = 14
9.(x + 12) = 149 - 14
9.(x + 12) = 135
x + 12 = 135 : 9
x + 12 = 15
x = 15 - 12 = 3
c,(x + 9).(x + 7) = 143
TH1: (x + 9) = 11 => x = 2
(x + 7) = 13 => x = 6
TH2: (x + 9) = 13 => x = 4
(x + 7) = 11 => x = 4
TH3: (x + 9) = -11 => x = -20
(x + 7) = -13 => x = -20
TH4: (x + 9) = -13 => x = -22
(x + 7) = -11 => x = -18
NA
21 tháng 7 2016
Gọi tập hợp con là A.
\(A=\left\{a,b\right\}\)
Gọi tập hợp con là B.
\(B=\left\{b,c\right\}\)
Gọi tập hợp con là C.
\(C=\left\{a,c\right\}\)
21 tháng 10 2016
A = 1 + 2 + 22 + 23 +.... + 239
= (1+2+22 + 23) + (24+25+26+27) + ... + (236+237+238+239)
= 15 + 24(1+2+22+23) + ... + 236(1+2+22+23)
= 15(24+...+236) \(⋮\)15
T = 1257 - 259
= 1257 - 1256
= 1256(125-1)
= 1256.124 \(⋮\) 124
M = 7 + 72 + 73 + ... + 72000
= (7+72) + (73+74) + ... + (71999+72000)
= 7(1+7) + 73(1+7) + ... + 71999(1+7)
= 8(7+73+...+71999) \(⋮\) 8
P = a + a2 + a3 + ... + a2n
= chưa nghĩ ra~
21 tháng 10 2016
còn phần cuối t xin
P=a+a2+...+a2n
=(a2+a)+...+(a2n+a2n-1)
=a(a+1)+...+a2n-1(a+1)
=(a+1)*(a+...+a2n-1) chia hết a+1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 1 2024
Bài 4:
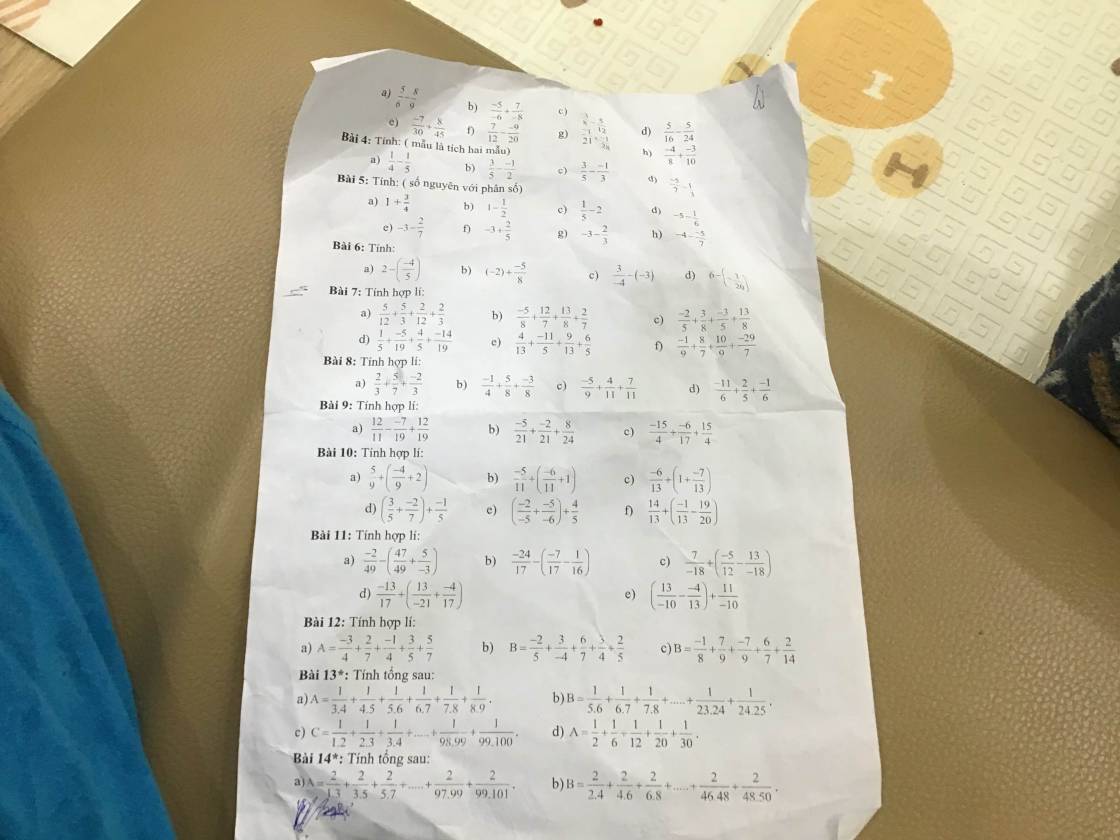
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 1 2024
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)
Q
7 tháng 7 2017
3/ Chu vi hình chữ nhật:
\(\left(\dfrac{1}{4}+\dfrac{3}{10}\right)\cdot2=\dfrac{11}{10}\) (chưa biết đơn vị)
Diện tích hình chữ nhật:
\(\dfrac{1}{4}\cdot\dfrac{3}{10}=\dfrac{11}{20}\) (chưa biết đơn vị)
2/3
-3/4