Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có A 7 5 = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 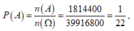

lại lần nữa:
Để mình làm lại :
Số cách xếp bất kỳ 13 học sinh là: \(\left|\Omega\right|=P_{13}\)
Số cách xếp có ít nhất 2 học sinh nữ cạnh nhau là: \(2.P_{12}\)
Số cách xếp không có 2 học sinh nữ cạnh nhau là:
\(P_{13}-2P_{12}=11P_{12}\)
Goi A là biến cố không có 2 học sinh nữ cạnh nhau
\(\Rightarrow\left|A\right|=11.P_{12}\)
\(\Rightarrow P\left(A\right)=\)\(\frac{\left|A\right|}{\left|\Omega\right|}\)\(=\frac{11}{13}\)
Tại sao chỗ xếp ít nhất 2 banj nữ cạnh nhau lại là P12.Nếu đã sắp xếp 2 bạn nữ đứng cạnh nhau rồi thì chỉ còn 11 bạn và sắp xếp theo cách 11! thôi chứ.Là 2!.11!,tại s lại là 2.12!??

Đáp án B
– Số phần tử của không gian mẫu n Ω =10!
* Xếp 10 học sinh trên một hàng ngang sao cho 5 học sinh nam xen kẽ 5 học sinh nữ có 2 cách xếp.
* Xét trong 2 cách xếp trên các khả năng Hoàng và Lan đứng liền kề nhau:
+ Xếp 8 học sinh trên một hàng ngang sao cho 4 học sinh nam xen kẽ 4 học sinh nữ có 2 cách xếp.
+ Với mỗi cách xếp 8 học sinh trên có 9 khoảng trống tạo ra. Với mỗi khoảng trống trên, xếp Hoàng và Lan vào khoảng trống này để được 5 học sinh nam xen kẽ 5 học sinh nữ có 1 cách xếp.
xxxx
Suy số cách xếp 5 học sinh nam xen kẽ 5 học sinh nữ mà Hoàng và Lan đứng kề nhau là: 2.9
Vậy số phần tử của A là: n =2-2.9=18432.


Chọn B
Số phần tử của không gian mẫu là ![]()
Sắp 5 học sinh nam thành một hàng ngang, có 5! cách (tạo ra khoảng trống).
Chọn 3 khoảng trống trong 6 khoảng trống để xếp 3 nữ, có C 6 3 cách chọn. Khi đó, số cách xếp 3 bạn nữ là C 6 3 .3! cách.
Vậy xác suất cần tìm là 

Đáp án C
Số cách xếp ngẫu nhiên là 10!.
Ta tìm số cách xếp thoả mãn:
Đánh số hàng từ 1 đến 10. Có hai khả năng:
5 nam xếp vị trí lẻ và 5 nữ xếp vị trí chẵn có 5!x5!= 120 2
5 nam xếp vị trí chẵn và 5 nữ xếp vị trí lẻ có 5!x5!= 120 2
Theo quy tắc cộng có 120 2 + 120 2 =2x 120 2 cách xếp thoả mãn.
Vậy xác suất cần tính 2 ( 5 ! ) 2 10 ! = 1 126

Chọn C
Chọn mỗi tổ hai học sinh nên số phần tử của không gian mẫu là ![]()
Gọi biến cố A: “Chọn 4 học sinh từ 2 tổ sao cho 4 em được chọn có 2 nam và 2 nữ”
Khi đó, xảy ra các trường hợp sau:
TH1: Chọn 2 nam ở Tổ 1, 2 nữ ở Tổ 2. Số cách chọn là ![]()
TH2: Chọn 2 nữ ở Tổ 1, 2 nam ở Tổ 2. Số cách chọn là ![]() .
.
TH3: Chọn ở mỗi tổ 1 nam và 1 nữ. Số cách chọn là ![]()
Suy ra, n(A) = ![]()
Xác suất để xảy ra biến cố A là: ![]()


Đáp án D.