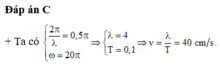
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
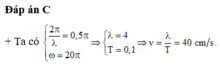
\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)
Đáp án B
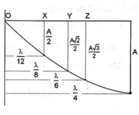
Biên độ tại bụng sóng: A= 2mm
Tại điểm có biên độ 2 mm
Khoảng cách từ Y đến bụng sóng
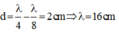
Tại điểm cách nút 4cm:
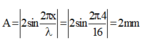(bụng sóng)
Vận tốc dao động của điểm trên dây cách nút 4cm
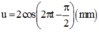
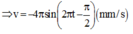
Tại thời điểm 1s: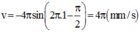 
\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.
\(u = 40 \sin (2,5\pi x)\cos (\omega t) ;(m,s)\)
So sánh với phương trình tổng quát: \(u = a \sin (\frac{ 2\pi x}{\lambda}+ \varphi)\cos (\omega t+\varphi_1 ) ;(m,s)\)
=> \(2,5\pi = 2\pi\frac{x}{\lambda}\)
=> \(\lambda = 0,8m.\)
Biên độ của điểm N cách một nút sóng 10 cm = 0,1 m là \(a_N = 40 \sin (2,5.\pi.0,1) = \frac{40}{\sqrt{2}}.\)
0 A 2 40 -40
khoảng thời gian ngắn nhất giữa 2 lần liên tiếp để một điểm trên bụng có độ lớn li độ bằng biên độ của điểm N là
=> Góc quay được kí hiệu màu đỏ.
\(t = \frac{\varphi}{\omega} = \frac{2.\pi/4}{2\pi T} = \frac{T}{4}s. \)
mà \(t = 0,125s=> T = 0,5s.\)
=> \(v = \frac{\lambda}{T} = \frac{0,8}{0,5}=1,6m/s=160cm/s.\)
Chọn đáp án.B.160cm/s.
