Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn: Chọn đáp án B
Giai đoạn 1: Hòn đá rơi tự do.
Giai đoạn 2: Hòn đá chạm vào đáy giếng phát ra âm thanh truyền đến tai người
Thời gian vật rơi: h = g t 1 2 2 ⇒ t 1 = 2 h g = 2.11 , 25 10 = 1 , 5 s Thời gian âm truyền từ đáy đến tai người: t 2 = h v = 11 , 25 300 = 0 , 0375 s
⇒ t 1 + t 2 = 1 , 5375 s

+ Thời gian hòn đá rơi tự do xuống tới đáy là: t 1 = 2 h g
+ Thời gian âm thanh vọng lên tới tai người là: t 2 = h v
+ t1 + t2 = 2 h 9 , 9 + h 330 = 3 → h ≈ 41 m
Đáp án D

Đáp án A.
Lời giải chi tiết:
Gọi độ sâu của giếng là h.
Thời gian hòn đá rơi tự do: 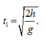
Thời gian âm thanh đi từ đáy lên miệng giếng: ![]()
Thời gian tổng cộng


Đáp án: D
HD Giải:
Thời gian hòn đá rơi tự do trong giếng là: 
Thời gian sóng âm truyền lại tai người sau khi va chạm vào đáy giếng là: 
Ta có phương trình: 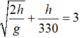
=> h = 41m

Khi đổ dần nước vào ống nghiệm đến độ cao 30cm thì thấy âm được khuyếch đại rất mạnh, có nghĩa là khi đó hiện tượng sóng dừng xảy ra, âm nghe được to nhất do tại đáy ống hình thành một nút sóng, miệng ống hình thành một bụng sóng. Mặt khác, nước cao 30cm thì cột không khí cao 50cm. Từ đó ta có:
\(300\left(\frac{1}{4.850+k\frac{1}{2.850}}\right)\le0,5=\)\(\frac{\lambda}{4}+k\frac{\lambda}{2}=v\left(\frac{1}{4f}+k\frac{1}{2f}\right)\le350\left(\frac{1}{4.850}\right)\)\(\Rightarrow1,93\le k\le2,33\Rightarrow k=2\)
\(\Rightarrow v=\frac{0,5}{\frac{1}{4.850+2.\frac{1}{2.850}}}=340\)
Từ đó dễ thấy \(\lambda\) = 40cm
Khi tiếp tục đổ nước vào ống thì chiều dài cột kí giảm dần, và để âm khuyếch đại mạnh thì chiều dài cột khí phải thỏa mãn
\(0< l=\frac{\lambda}{4}+k\frac{\lambda}{2}=10+k.20< 50\)
\(-0,5< k< 2\)
k = 0;1
Vậy khi đổ thêm nước vào thì có thêm 2 vị trí làm cho âm khuyếch đại rất mạnh
chọn A
Trước tiên ta thấy rằng trong ống lúc đổ nước và đến độ cao 30cm thì có sóng dừng giống sợi dây 1 đầu cố định, 1 đầu tự do.
Vậy ta có : \(l=\left(2k+1\right)\lambda\Rightarrow\lambda=\frac{4l}{\left(2k+1\right)}\) (2)
Mặt khác ta có: \(v=\lambda f\) (1)
Từ (1) và (2) ta có:
\(v=\frac{4lf}{2k+1}=\frac{4\left(0,8-0,3\right)850}{2k+1}=\frac{1700}{2k+1}\)
Vì vận tốc truyền âm nằm trong khoảng:
\(300\le v\le500\Rightarrow300\le\frac{1700}{2k+1}\le350\Rightarrow1,9\le k\le2,3\Rightarrow k=2\)
Vậy vận tốc truyền âm và bước sóng của âm là:
\(v=\frac{1700}{2.2+1}=340\left(\frac{m}{s}\right)\Rightarrow\lambda=\frac{v}{f}=0,4m=40cm\)
Như vậy tính cả miệng ống thì có 3 bụng sóng. Vì:
\(l=\left(2n+1\right)\frac{\lambda}{4}\Rightarrow\pi=\frac{4.50}{2.40}-0,5=2\)
N = 2+1=3 Vậy sẽ có 3 vị trí.
Vậy B đúng

Tốc độ góc \(\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{20}{0,2}}=10\left(rad/s\right)\)
Lại có \(A=\sqrt{\frac{v^2}{\omega^2}+\frac{a^2}{\omega^4}}=\sqrt{\frac{20^2}{10^2}+\frac{\left(2\sqrt{3}.100\right)^2}{10^4}}=4\left(cm\right)\)

Hướng dẫn: Chọn đáp án C