Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi chiều dài là a, chiều rộng là b.
Nửa chu vi hình chữ nhật là : \(\dfrac{94,4}{2}=47,2\left(m\right)\)
Ta có hệ pt : \(\left\{{}\begin{matrix}a+b=47,2\\a\cdot b=494,55\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=47,2-b\\\left(47,2-b\right)\cdot b=494,55\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=47,2-b\\47,2b-b^2=494,55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=47,2-15,7=31,5\\b=15,7\left(giải-HPT-bậc-2\right)\end{matrix}\right.\)
Vậy chiều dài là 31,5 mét, chiều rộng 15,7 mét.
b) Vẫn gọi chiều dài là a, chiều rộng là b.
Có hpt : \(\left\{{}\begin{matrix}a-b=12,1\\a\cdot b=1089\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=12,1+b\\\left(12,1+b\right)\cdot b=1089\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=12,1+b\\12,1b+b^2=1089\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=12,1+27,5=39,6\\b=27,5\left(Giải-HPT-Bậc-2\right)\end{matrix}\right.\)
Vậy chiều dài là 39,6 mét, chiều rộng là 27,5 mét.

Diện tích mỗi phần:
\(\left(\frac{15}{4}\cdot\frac{2}{3}\right):5=\frac{1}{2}\left(m^2\right)\)
Đáp số : \(\frac{1}{2}m^2\)

Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là x (m), y (m). (điều kiện x > y > 0)
a) Theo đề bài:
Chu vi là 94,4m nên ta có phương trình: 2(x + y) = 94,4 (1)
Diện tích là 494,55m2 nên ta có phương trình: x.y = 494,55 (2)
Từ (1) và (2) ta có hệ:
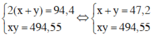
Giải hệ phương trình trên:
Cách 1: Dựa vào định lý Vi–et đảo
Từ hệ phương trình suy ra x, y là nghiệm của phương trình:
X2 – 47,2X + 494,55 = 0
Giải phương trình ta được: X1 = 31,5 và X2 = 15,7
Vì x > y nên x = 31.5 và y = 15.7
Cách 2: Phương pháp thế
Từ x + y = 47,2 ⇒ x = 47,2 – y, thay vào phương trình x.y = 494,55 ta được:
(47,2 – y).y = 494,55
⇔ 47,2.y – y2 = 494,55
⇔ y2 – 47,2y + 494,55 = 0
⇔ y = 31.5 hoặc y = 15.7
Nếu y = 31.5 ⇒ x = 15.7 (loại vì x < y)
Nếu y = 15.7 ⇒ x = 31.5 (thỏa mãn).
Vậy hình chữ nhật có chiều dài bằng 31.5m và chiều rộng bằng 15.7m
b) Theo đề bài:
Hiệu của hai cạnh là 12,1 m nên ta có phương trình: x – y = 12,1 (3)
Diện tích là 1089m2 nên ta có phương trình: x.y = 1089 (4)
Từ (3) và (4) ta có hệ: 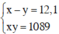
Từ (3) ⇒ x = 12,1 + y, thay vào (4) ta được:
(12,1 + y).y = 1089
⇔ y2 + 12,1.y – 1089 = 0
⇔ y = 27,5 (t/m) hoặc y = –39,6 (loại)
⇒ x = 12,1 + 27,5 = 39,6
Vậy hình chữ nhật có chiều dài 39,6m và chiều rộng 27,5m

a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.

Chỉ lm bài thoii, hình bn tự vẽ nha !!!
\(a.\) Tứ giác \(BEDC\) có \(\widehat{BEC}=\widehat{BDC}=90^0\)
Suy ra tứ giác \(BEDC\) là tứ giác nội tiếp
Tam giác \(DBA\) vuông tại \(D\) có đường cao \(DL\) nên suy ra \(BD^2=BL.BA\)
\(b.\) Tứ giác \(ADEH\) có:
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\) nên tứ giác \(ADEH\) nội tiếp
Từ đó \(\widehat{BAK}=\widehat{BDE}\)
Mà \(\widehat{BJK}=\widehat{BAK}\) ( 2 góc nội tiếp cùng chắn một cung )
Do đó \(\widehat{BJK}=\widehat{BDE}\)

a) △ = \(m^2-28\ge0\)\(\Leftrightarrow\left[{}\begin{matrix}m\ge\sqrt{28}\\m\le-\sqrt{28}\end{matrix}\right.\)
Theo Vi-ét \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2+x_2^2+2x_1x_2=m^2\\x_1x_2=7\end{matrix}\right.\)
\(\Rightarrow m^2=24\)\(\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{24}\\m=-\sqrt{24}\end{matrix}\right.\)(không thỏa mãn)
b) △ = \(4-4\left(m+2\right)\ge0\)\(\Leftrightarrow m\le-1\)
Theo Vi-ét \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m+2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2+x_2^2+2x_1x_2=4\\x_1x_2=m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_2-x_1\right)^2+4x_1x_2=4\\x_1x_2=m+2\end{matrix}\right.\)
\(\Rightarrow4+4\left(m+2\right)=4\)\(\Leftrightarrow m=-2\)(thỏa mãn)
c) △ = \(\left(m-1\right)^2-4\left(m+6\right)\)\(\ge0\)\(\Leftrightarrow m^2-2m+1-4m-24\ge0\)
\(\Leftrightarrow m^2-6m-23\ge0\)
\(\Leftrightarrow\left(m-3\right)^2\ge32\)\(\Leftrightarrow\left[{}\begin{matrix}m\ge\sqrt{32}+3\\m\le-\sqrt{32}+3\end{matrix}\right.\)
Theo Vi-ét \(\left\{{}\begin{matrix}x_1+x_2=1-m\\x_1x_2=m+6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2+x_2^2+2x_1x_2=m^2-2m+1\\x_1x_2=m+6\end{matrix}\right.\)
\(\Rightarrow10+2\left(m+6\right)=m^2-2m+1\)
\(\Leftrightarrow m^2-4m-21=0\)\(\Leftrightarrow\left(m+3\right)\left(m-7\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=7\\m=-3\end{matrix}\right.\)\(\Leftrightarrow m=-3\)(thỏa mãn)
mấy câu kia cũng dùng Vi-ét xử tiếp nha

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là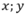 (m)
(m) 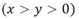
Theo đề bài ta có: