Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
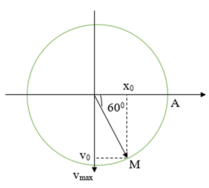
Chu kì dao động của vật:
T = 2 ( t 2 − t 1 ) = 1 , 5 s
v t b = 2 A Δ t ⇒ A = v t b Δ t 2 = 6 c m
Thời điểm t 1 = 1,75s ứng với góc
Δ φ = ω t 1 = 7 π 3 = 2 π + π 3 .
Giả sử thời điêm t 1 vật đang ở biên dương, sử dụng quay ngược lại trước đó 7 π / 3 rad ta xác định được thời điểm t 0 như hình vẽ. Từ đó ta suy ra:
x 0 v 0 = A 2 3 2 v max = 3 4 ω A 2 = 12 π 3

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Đáp án A
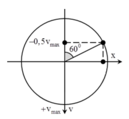
Chu kì dao động của vật T = 2 ( t 2 - t 1 ) = 1,5 s
v t b = 2 A ∆ t ⇒ A = v t b . ∆ t 2 = 6 c m
Thời điểm t = 0 ứng với góc lùi ∆ φ = ω t 1 = 7 π 3 = 2 π + π 3
Từ hình vẽ ta có x 0 v 0 = - v m a x 2 3 2 A = - 3 4 ω A 2 = - 12 π 3

Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2,5^2+\dfrac{(50\sqrt 3)^2}{\omega^2}=(2,5\sqrt 3)^2+\dfrac{50^2}{\omega^2}\)
\(\Rightarrow \omega = 20(rad/s)\)
Và \(A=5cm\)
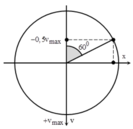

 chọn A
chọn A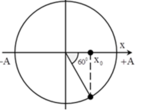

Đáp án A