Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có : \(S=x_1+x_2=\dfrac{7}{2};P=x_1x_2=1\)
b) ta có \(S=x_1+x_2=\dfrac{-9}{2};P=x_1x_2=\dfrac{7}{2}\)
c) ta có : \(S=x_1+x_2=\dfrac{-4}{2-\sqrt{3}};P=x_1x_2=\dfrac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) ta có : \(S=x_1+x_2=\dfrac{3}{1,4}=\dfrac{15}{7};P=x_1x_2=\dfrac{1,2}{1,4}=\dfrac{6}{7}\)
e) ta có : \(S=x_1+x_2=\dfrac{-1}{5};P=x_1x_2=\dfrac{2}{5}\)
a) Theo hệ thức Vi-ét :
x1+x2=\(\frac{-b}{a}=\frac{7}{2}\)
x1x2=\(\frac{c}{a}=\frac{2}{2}=1\)
b) theo hệ thức Vi-ét:
x1+x2=\(\frac{-b}{a}=\frac{-9}{2}\)
x1x2=\(\frac{c}{a}=\frac{7}{2}\)
c)x1+x2=\(\frac{-b}{a}=\frac{-4}{2-\sqrt{3}}=-8-4\sqrt{3}\)
x1x2=\(\frac{c}{a}=\frac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) x1+x2=\(\frac{-b}{a}=\frac{3}{1,4}=\frac{15}{7}\)
x1x2=\(\frac{c}{a}=\frac{1,2}{1,4}=\frac{6}{7}\)
e) x1+x2=\(\frac{-b}{a}=\frac{-1}{5}\)
x1x2=\(\frac{c}{a}=\frac{2}{5}\)

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 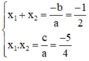
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 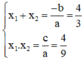
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 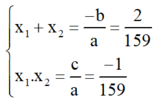

a) Phương trình 4x2 + 2x – 5 = 0 có nghiệm vì a = 4, c = -5 trái dấu nhau nên
x1 + x2 = \(-\dfrac{1}{2}\), x1x2 = \(-\dfrac{5}{4}\)
b) Phương trình 9x2 – 12x + 4 = 0 có ∆' = 36 - 36 = 0
x1 + x2 = \(\dfrac{12}{9}\) = \(\dfrac{4}{3}\), x1x2 = \(\dfrac{4}{9}\)
c) Phương trình 5x2+ x + 2 = 0 có ∆ = 12 - 4 . 5 . 2 = -39 < 0
Phương trình vô nghiệm, nên không tính được tổng và tích các nghiệm.
d) Phương trình 159x2 – 2x – 1 = 0 có hai nghiệm phân biệt vì a và c trái dấu
x1 + x2 = \(\dfrac{2}{159}\), x1x2 = \(-\dfrac{1}{159}\)
a) Phương trình 4x2 + 2x – 5 = 0 có nghiệm vì a = 4, c = -5 trái dấu nhau nên
x1 + x2 = , x1x2 =
b) Phương trình 9x2 – 12x + 4 = 0 có ∆' = 36 - 36 = 0
x1 + x2 = =
, x1x2 =
c) Phương trình 5x2+ x + 2 = 0 có ∆ = 12 - 4 . 5 . 2 = -39 < 0
Phương trình vô nghiệm, nên không tính được tổng và tích các nghiệm.
d) Phương trình 159x2 – 2x – 1 = 0 có hai nghiệm phân biệt vì a và c trái dấu
x1 + x2 = , x1x2 =

\(\text{ĐK: }x^3-6x^2+12x-8=\left(x-2\right)^3\ne0\Leftrightarrow x\ne2\)
\(pt\Leftrightarrow\frac{\left(x-2\right)^3\left(x^2-3x-3\right)}{\left(x-2\right)^3}=0\Leftrightarrow x^2-3x-3=0\)
Vậy pt có 2 nghiệm \(a;b\) thỏa \(a+b=3;\text{ }a.b=-3\text{ (Vi-et)}\)
\(A=\frac{1}{a^{10}}+\frac{1}{b^{10}}=\frac{a^{10}+b^{10}}{\left(ab\right)^{10}}=\frac{\left(a^5+b^5\right)^2-2a^5b^5}{\left(-3\right)^{10}}\)
Ta có: \(a^5+b^5=\left(a+b\right)\left(a^4-a^3b+a^2b^2-ab^3+b^4\right)\)
\(=\left(a+b\right)\left[\left(a^4+b^4+2a^2b^2\right)-a^2b^2-ab\left(a^2+b^2\right)\right]\)
\(=\left(a+b\right)\left[\left(a^2+b^2\right)^2-ab\left(a^2+b^2\right)-a^2b^2\right]\)
\(=\left(a+b\right)\left\{\left[\left(a+b\right)^2-2ab\right]^2-ab\left[\left(a+b\right)^2-2ab\right]-\left(ab\right)^2\right\}\)
\(=3\left[\left(3^2-2.\left(-3\right)\right)^2-\left(-3\right)\left(3^2-2.\left(-3\right)\right)-\left(-3\right)^2\right]\)
\(=783\)
\(A=\frac{783^2-2\left(-3\right)^5}{3^{10}}=\frac{2525}{243}\)

a) Điều kiện xác định \(16x+8\ge0\Leftrightarrow x\ge-\frac{1}{2}.\)
Theo bất đẳng thức Cô-Si cho 4 số ta được
\(4\sqrt[4]{16x+8}=4\sqrt[4]{2\cdot2\cdot2\cdot\left(2x+1\right)}\le2+2+2+2x+1=2x+7\)
Do vậy mà \(4x^3+4x^2-5x+9\le2x+7\Leftrightarrow\left(2x-1\right)^2\left(x+2\right)\le0\).
Vì \(x\ge-\frac{1}{2}\to x+2>0\to\left(2x-1\right)^2\le0\to x=\frac{1}{2}.\)
b. Ta viết phương trình dưới dạng sau đây \(9x^4-21x^3+27x^2+16x+16=0\Leftrightarrow3x^2\left(3x^2-7x+7\right)+4\left(x+2\right)^2=0\)
Vì \(3x^2-7x+7=\frac{36x^2-2\cdot6x\cdot7+49+35}{12}=\frac{\left(6x-7\right)^2+35}{12}>0\) nên vế trái dương, suy ra phương trinh vô nghiệm.

Phương trình 5x2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 12 – 4.2.5 = -39 < 0
⇒ Phương trình vô nghiệm.
Phương trình 9x2 – 12x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)2 – 4.9 = 0
⇒ Phương trình có nghiệm kép x1 = x2.
Theo hệ thức Vi-et ta có: