
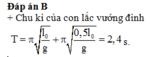
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

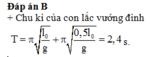

Đáp án B
+ Chu kì của con lắc vướng đinh T = π l 0 g + π 0 , 5 l 0 g = 2 , 4

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Chiều dài l thì chu kì dao động là: \(T=2\pi\sqrt[]{\frac{l}{g}}\)= 2 (s)
Chiều dài \(\frac{l}{2}\) thì chu kì dao động là:
\(T'=2\pi\sqrt[]{\frac{l}{2.g}}\)\(=\frac{T}{\sqrt{2}}=\sqrt{2}\left(s\right)\)
Khi dây treo vướng đinh thì dao động con lắc là dao động tuần hoàn gồm một nửa dao động điều hòa với chiều dài l và một nửa dao động với chiều dài \(\frac{l}{2}\)
Chu kì dao động là:
T1
\(=\frac{T+T'}{2}=\frac{2+\sqrt{2}}{2}\)

1/ Chu kì con lắc đơn:
\(T=2\pi\sqrt{\dfrac{\ell}{g}}\)
Chiều dài tăng 25% thì:
\(T'=2\pi\sqrt{\dfrac{\ell+0,25\ell}{g}}=1,12.2\pi\sqrt{\dfrac{\ell}{g}}=1,12T\)
Suy ra chu kì tăng 12%

Đáp án A
+ Tốc độ của vật khi đi qua vị trí cân bằng v = v max = 2 gl 1 − cosα 0 = 4 , 03