Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xu dùng để tích lũy mua VIP, mua vật phẩm trên shop OLM và shop HOC24 (sẽ ra mắt trong thời gian tới) các em nhé!
Cô ơi, cho em xin phép phản hồi 1 chút về web ạ!
Là từ nãy giờ, khi em đang thi đấu ở trong web, nó liên tục ghi bảng "Lỗi QLIB: undefined" và dừng tải câu hỏi, em đã load lại trang gần như rất nhiều lần, và internet nhà em cũng không có vấn đề gì cả ạ, nhưng mà đề ở trên đó vẫn không hiện lên ạ:((cái này lặp đi lặp lại 2, 3 lần rồi, vẫn không khắc phục được ạ! Em đã xem xét từ nãy giờ rất kĩ, nhưng không có vấn đề gì về phần của em ạ!Mong các thầy cô xử lý lỗi này để tránh trường hợp các bạn học sinh khác cũng vào thi sẽ gặp lỗi mạng, và không thể tiếp tục cuộc thi ạ! Đó là 1 số ý kiến riêng của em, mong mọi người sẽ khắc phục lỗi sớm hơn ạ!
Rep bài viết sơm, Chúc mn cuối tuần vv .
Tranh thủ e vào xin ít vía cho tối nay cho lên top ak.

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

😉 Các bạn nhanh tay tham gia ở đây https://www.facebook.com/olm.vn để giật giải thưởng siêu to khổng lồ nha 😁
1 con gấu là: 36 : 3 = 12
1 cái bánh là: ( 26 - 12 ) : 2 = 7
1 Chùm nho là : (15 - 7 ) : 2 = 4
1 con gấu - 1 cái bánh + 1chùm nho
hay: 12 - 7 + 4 = 9

a)\(\sqrt{81}-\sqrt{80}\)\(.\sqrt{0,2}\)\(=\sqrt{9^2}-\sqrt{80.0,2}\)\(=9-\sqrt{16}\)\(=9-4=5\)
\(\sqrt{\left(2-\sqrt{5}\right)^2}\)\(-\frac{1}{2}.\sqrt{20}\)\(=|2-\sqrt{5}|-\frac{1}{2}.\sqrt{4.5}\)\(=2-\sqrt{5}-\frac{1}{2}.2\sqrt{5}\)
\(=2-\sqrt{5}-\sqrt{5}=2\)
Tôi lm đc đến đây thôi(@_@)
\(\)

a) Vì \(\left|A+B\right|\ge0\)và \(\left|A\right|+\left|B\right|\ge0\)
Bình phương 2 vế ta có:
\(\left|A+B\right|^2\le\left(\left|A\right|+\left|B\right|\right)^2\)
\(\Leftrightarrow A^2+2AB+B^2\le A^2+2\left|AB\right|+B^2\)
\(\Leftrightarrow2\left|AB\right|\ge2AB\)\(\Leftrightarrow\left|AB\right|\ge AB\)(1)
Theo tính chất của dấu giá trị tuyệt đối thì \(\left|AB\right|\ge AB\)
\(\Rightarrow\)(1) luôn đúng \(\Rightarrow\left|A+B\right|\le\left|A\right|+\left|B\right|\)( đpcm )
Dấu " = " xảy ra \(\Leftrightarrow AB\ge0\)
b) \(M=\sqrt{x^2+4x+4}+\sqrt{x^2-6x+9}=\sqrt{\left(x+2\right)^2}+\sqrt{\left(x-3\right)^2}\)
\(=\left|x+2\right|+\left|x-3\right|=\left|x+2\right|+\left|3-x\right|\)
Áp dụng kết quả phần a ta có:
\(M=\left|x+2\right|+\left|3-x\right|\ge\left|x+2+3-x\right|=\left|5\right|=5\)
Dấu " = " xảy ra \(\Leftrightarrow\left(x+2\right)\left(3-x\right)\ge0\)
TH1: \(\hept{\begin{cases}x+2\ge0\\3-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge-2\\x\le3\end{cases}}\Leftrightarrow-2\le x\le3\)
TH2: \(\hept{\begin{cases}x+2< 0\\3-x< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< -2\\x>3\end{cases}}\)( vô lý )
Vậy \(minM=5\)\(\Leftrightarrow-2\le x\le3\)
a) Do 2 vế của BĐT không âm nên ta có:
\(\left|A+B\right|\le\left|A\right|+\left|B\right|\Leftrightarrow\left|A+B\right|^2\le\left(\left|A\right|+\left|B\right|\right)^2\)
\(\Leftrightarrow A^2+B^2+2AB\le A^2+B^2+2\left|AB\right|\Leftrightarrow AB\le\left|AB\right|\) (LUÔN ĐÚNG)
Dấu '=' xảy ra <=> \(AB\ge0\)

Bài 4 :
a, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm
Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm
b, Xét tam giác ABK vuông tại A, đường cao AD
\(AB^2=BD.BK\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2=BH.BC\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(BD.BK=BH.BC\)(3)
c, Xét tam giác BHD và tam giác BKC
^B _ chung
(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)
Vậy tam giác BHD ~ tam giác BKC ( c.g.c )
=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4)
Ta có : cosABD = \(\frac{DB}{AB}\)
=> cos2ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos2ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)
=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)
\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4)
=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)
Bài 3 :
a, Với \(x>0;x\ne1\)
\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)



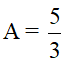
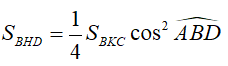
Dạ cô, để tối nay nếu con rảnh thì con sẽ vô ạ
có cần vip ko cô